This will be another post about the mysterious Voynich Manuscript, with apologies to those of my readers and subscribers whose cup of tea this isn’t. If you’re new to the topic, you may wish to find a different entry point, since I’ll be picking things up here some distance down the rabbit hole already.
I’ve been trying lately to come up with some way to analyze Voynichese text that can accommodate patterning on multiple levels simultaneously—what glyphs can be adjacent to each other, what word structures are valid, what sequences of words are most probable, what phenomena tend to appear in particular parts of lines, and what phenomena tend to appear in particular parts of paragraphs. The patterning we can detect on all these levels seems just as likely to be interconnected somehow as not, and perhaps even to result straightforwardly from the interplay among a relatively simple set of rules. And if that’s true, then I’m not sure we should be able to account satisfactorily for any one of the levels by itself without accounting for all of the levels at once; for example, it might not be possible to formulate a fully satisfactory “word grammar” in isolation from considerations of line and paragraph structure if these all depend to some degree upon one another. With that in mind, I’ve started trying to develop a scalable model around individual choices of glyph and whatever contextual features can be shown to affect their probabilities, whether closer by or more distant. Some pieces of this model have been easy enough to tackle, while others still seem almost impossibly difficult. But so far it’s been feeling like a promising approach overall—maybe as a kind of brute-force pattern detection mechanism, if nothing else.
In what follows, I’ll be treating ch, Sh, cTh, cPh, cKh, and cFh as indivisible units for purposes of analysis. Like many other people, though, I’ve had some trouble coming up with a good strategy for handling i and e, which routinely appear repeated next to each other. It wouldn’t make much sense just to assess the probability of, say, one i following another i, given that double ii is actually more common than single i. What I’ve done—where applicable—is first to assess the probability of a transition to any quantity of e or i, and then to assess the probability of a specific quantity of e or i as a separate step. For example, I might first consider the probability of che, chee, or cheee as opposed to cha, cho, etc.; and then, afterwards, the probability of che, chee, or cheee specifically.
§ 1
Microscale Analysis
Let’s kick things off with the following question:
Given one glyph of any particular type, what is the probability—expressed as a percentage—that the next glyph will be of a particular type, ignoring spaces?
This amounts to trying to analyze Voynichese glyph sequences as first-order Markov chains, by means of first-order Markov modeling. I’ll acknowledge up front that this approach is too simple to account for every detectable pattern, and that the picture which emerges from it will be a bit simplified and stylized. But sometimes a simplified and stylized picture can be heuristically useful, so I hope you’ll indulge my experiment with that in mind. Some terminology:
- Any given permutation of two glyphs such as k_a is a bigram.
- The step rightward from one glyph to another, such as from k to a, is a transition. We can notate this as k>a to distinguish it from k_a as a bigram.
- The probability of a transition from one glyph to another, such as k>a, is its transitional probability, not to be confused with the frequency of the k_a bigram itself.
- The whole set of probabilities of different glyphs following after any one given glyph, such as the probabilities of all different glyphs following after k, constitute that glyph’s transitional probability matrix, with the total adding up to 100%.
I know there have already been plenty of studies of Voynichese in terms of its frequencies and probabilities and entropy (a good entry-point to which can be found here), but these generally seem to have pursued higher-level questions formulated with natural-language plaintext as their point of reference: whether the text obeys Zipf’s Law, how its overall statistics compare to those of texts in languages such as Latin, Hebrew, or Hawaiian, and so on. Meanwhile, past efforts to model finer structural details have tended to focus primarily on the morphology of “words,” or glyph sequences with space on either side. Rather than trying to work out an independent transitional probability matrix for each glyph, these efforts have typically proceeded by identifying series of “slots” and then tallying the various configurations of these “slots” and the various glyphs or combinations of glyphs that can fill each of them. Jorge Stolfi’s work is the paradigmatic example (no pun intended).
But I’ve been looking for a way to develop a different kind of morphology ever since I began to suspect that the patterns we should be interested in may not respect word boundaries. After all, the spaces don’t seem as though they could carry much if any meaning. It’s not unusual for them to be visually ambiguous, and if we were to remove all of them, we could reconstruct where they go with over 95% accuracy by inserting them according to the following rules (introduced in an earlier post, at section four):
- Before q
- After g, m, n
- After r except before y, i
- After s before ch (with or without inserted gallows), Sh, d, l
- After y except before t, k
- After l before r, o, d, ch (with or without inserted gallows), Sh
- Between repetitions of o, s, l
Even the vast majority of exceptions to the above rules involve fewer than twenty specific bigrams starting with l, r, y, o, and s, and the same bigrams also tend to be spaced ambiguously the most often, judging from the incidence of “comma breaks” in the Zandbergen transcription. There thus appears to be a distinction inherent to the script itself between strong breakpoints which are pretty much obligatory and ambivalent breakpoints which can go either way. These patterns seem as consistent as any associated with a conventional “word grammar,” but if we limit our study to the forms of discrete words, we won’t detect them. Insofar as such patterns have been studied in the past, they’ve generally been approached in practice as the stuff of syntax rather than morphology (with notable contributions ranging from Prescott Currier to Emma May Smith and Marco Ponzi); that is, there’s the matter of how words are put together according to tight formal constraints, and then there’s the separate matter of tantalizing correlations between the endings of those words and the beginnings of the words that next follow them. Maybe these really are separate phenomena. But I don’t want to assume they are, and I’d like to analyze them in some way that can accommodate the possibility that they’re not. With that in mind, combining glyph-by-glyph transitional probabilities with spacing rules is the simplest strategy it occurs to me to try.
If we calculate a transitional probability matrix for each Voynichese glyph type, disregarding spaces, we find not only that each glyph favors some other glyph to follow it more than any others, but that it often does so by a wide margin over the next most preferred option. I’ll refer to the most probable transition for a given glyph as its “first option,” with other transitions ranked as “second option,” “third option,” and so forth.
Transitional probabilities are so strikingly different between the two “languages” Currier A and Currier B that there’s scarcely any value in calculating them across the whole manuscript. So let’s start by taking a look at a list of just the first and second options for each reasonably common glyph type in Currier B, together with the percentages of cases involved. Note that for glyphs in second position, I use i+ and e+ to indicate any quantity of i or e glyphs, following the logic laid out in my introduction. Although I give percentages to two decimal places because that’s what my scripts report, I don’t mean to imply that this degree of precision is meaningful.
- a>i+ (47.76%); a>r (23.60%)
- cFh>y (35.71%); cFh>e+ (25.00%)
- ch>e+ (57.94%); ch>o (11.99%)
- cKh>y (58.79%); cKh>e+ (24.18%)
- cPh>e+ (42.70%); cPh>y (17.98%)
- cTh>y (53.70%); cTh>e+ (23.55%)
- d>y (63.71%); d>a (25.87%)
- e>d (47.36%); e>y (19.85%)
- ee>d (39.79%); ee>y (37.96%)
- eee>y (50.38%); eee>d (27.48%)
- f>ch (52.38%); f>a (18.65%)
- g>a (28.57%); g>o (14.29%)
- i>n (72.16%); i>r (20.34%)
- ii>n (95.13%); ii>r (3.44%)
- iii>n (90.70%); iii>l (3.10%)
- k>e+ (41.86%); k>a (35.94%)
- l>k (19.85%); l>ch (19.73%)
- m>o (35.25%); m>ch (26.62%)
- n>o (33.11%); n>ch (26.05%)
- o>k (30.31%); o>l (23.25%)
- p>ch (55.95%); p>o (16.42%)
- q>o (97.69%); q>e+ (1.17%)
- r>a (29.25%); r>o (27.99%)
- s>a (47.18%); s>o (26.53%)
- Sh>e+ (68.81%); Sh>o (11.75%)
- t>e+ (33.74%); t>a (33.03%)
- y>q (28.11%); y>o (17.96%)
The transitions shown in blue involve relatively strong breakpoints, while the transitions shown in red involve relatively ambivalent ones (with at least 100 cases going each way in Currier B). Transitions that require or permit spacing tend to have weaker preferences for first options than transitions that almost always appear written together, but not overwhelmingly so, and not invariably. Meanwhile, the glyph n transitions ~59% of the time to either its first or second option—with a strong breakpoint—which isn’t far behind the ~61% we see for cPh or cFh, both of which strongly favor being written together with the following glyph. Thus, transitions between words appear to have constraints comparable to those within words. And transitions are rather tightly constrained on the whole. The only glyphs that don’t have at least a 50% probability of being followed by either their first or second option are l (~40%), y (~46%) and g (~44%).
If we now trace the most probable single course forward from glyph to glyph in Currier B—the path of least resistance, if you will—we discover the following closed loop:
- q>o (97.69%)
- o>k (30.31%)
- k>e+ (41.86%)
- more specifically k>ee (22.72%; 54.28% within k>e+)
- ee>d (39.79%)
- d>y (63.71%)
- y>q (28.11%)
This default loop generates the sequence qokeedyqokeedyqokeedyqokeedy….; and since there’s just one strong breakpoint at the adjacency y_q, and no ambivalent breakpoints, it would predictably appear broken up into words as qokeedy.qokeedy.qokeedy.qokeedy. Of course, this happens to resemble one of the most conspicuous kinds of repetitive pattern we actually see in Currier B.
Meanwhile, the most probable path leading forward from every glyph that isn’t itself in the qokeedy loop nevertheless leads into it sooner or later. Some reach it by way of e: ch>e, Sh>e, cPh>e. Others reach it by way of y (cFh>y, cKh>y, cTh>y) or k (l>k). Yet others reach it indirectly by way of ch>e: f>ch, and p>ch. And some reach it by way of o:
- a>i+ (47.76%)
- more specifically a>ii (26.65%; 55.80% within a>i+)
- ii>n (95.13%)
- n>o (33.11%)
The qokeedy loop is closed if we choose the most probable option for each transition within it, but it’s more likely to permit escape in some places than in others. Here are all the options we encounter as we pass through the loop with at least a 10% probability.
- q>o (97.69%)
- o>k (30.31%); second option = o>l (23.25%); third option = o>t (18.63%)
- k>e+ (41.86%); second option = k>a (35.94%)
- more specifically k>ee (22.72%; 54.28% within k>e+); second option = k>e (17.20%; 41.09% within k>e+)
- ee>d (39.79%); second option = ee>y (37.96%); third option = ee>o (11.98%)
- d>y (63.71%); second option = d>a (25.87%)
- y>q (28.11%); second option = y>o (17.96%); third option = y>ch (11.51%)
If we were to start at q and try taking each of these alternative options in turn, but all first options thereafter, we would hypothetically get:
- second option: qolkeedy.qokeedy….; third option: qotedy.qokeedy….
- second option: qokaiin.okeedy….
- second option: qokedy.qokeedy….
- second option: qokeey.qokeedy….; third option: qokeeokeedy….
- second option: qokeedaiin.okeedy….
- second option: qokeedy.okeedy….; third option: qokeedy.chedy….
Similarly, if we select some other starting glyph outside the loop, its path forward will present its own set of alternatives, as in this example:
- a>i (47.76%); second option = a>r (23.60%); third option = a>l (20.89%)
- within a>i, more specifically a>ii (26.65% of same total); second option = a>i (20.06% of same total)
- ii>n (95.13%)
- n>o (33.11%); second option = n>ch (26.05%); third option = n>Sh (13.81%)
If we were once again to try taking each of these alternative options in turn, but all first options thereafter, we would get:
- second option: ar.okeedy.qokeedy….; third option: alkeedy.qokeedy….
- second option: ain.qokeedy….
- second option: aiin.chedy.qokeedy….; third option: aiin.Shedy.qokeedy….
All this gives us a conceptually simple model of default behavior for Voynichese in which the tendency of the script is to repeat in an endless qokeedy loop unless it gets knocked out of it through a transition to some less probable option, as well as to fall back into the loop if and when it ever escapes from it.
So how do the model sequences I generated above for single-glyph deviations from the qokeedy loop match up against the actual text? A slim majority of them do in fact turn up multiple times, and we can generally find similar words and sequences to those that don’t.
- qokedy.qokeedy (15)
- qokeey.qokeedy (9)
- qokeedy.chedy (7)
- aiin.Shedy.qokeedy (6)
- qotedy.qokeedy (5)
- qokeedy.okeedy (4)
- aiin.chedy.qokeedy (4)
- ain.qokeedy (3)
- qokaiin.okeedy (1)
- ar.okeedy.qokeedy (1)
- qolkeedy.qokeedy (0), but qolkeedy.qokedy (3)
- qokeeokeedy (0), but qokeeoky (1); qokeokedy (1)
- qokeedaiin.okeedy (0), but qokeedaiin (2)
- alkeedy.qokeedy (0), but alkedy.qokedy (1); alkeedy (5)
I note in particular the similarity of the unattested qokeeokeedy to the words qokeeoky and qokeokedy, both of which would be considered irregular by most “word grammars.” It’s also worth mentioning that when I went searching for the predicted sequences, I seemed to find them turning up disproportionately often in Quire 13 (ff75-84) or Quire 20 (ff103-116).
We can also work in the other direction by taking actual glyph sequences from the text and seeing how our nascent model would analyze them. Here I’m going to draw on a dataset I created by removing all word and line breaks and identifying all glyph sequences that repeat exactly at least twice; I’ll call it the Repetition Dataset. It isn’t completely compatible with my present glyph adjacency analysis because it includes sequences that cross line breaks, but it’s still a handy point of reference. The longest exactly repeating sequences contained in it all seem to adhere rather closely to the qokeedy loop. All sequences in the following list occur twice unless otherwise stated.
- edyqokedyqokeedyqokeedy (plus another occurrence of just edyqokedyqokeedyqoke)
- olchedyqokainolSheyqokain
- okaiinShedyqokeedyqotedy
- edyqokaiinchedyqokeedyl
- keedyqokedyqokedyqoke
- edyqokeedycheedyqokeed
- edyqotedyqokeedyqokee
- edyqokeedyqokeedyqoke
- ealqokeedyqokeedyqoke
- olShedyqokedyqokeedyqo
- Shedyqokedyqokeedyqoke (3 occurrences; note overlap)
- Shedyqokedyqokeedyqot (note overlap)
- edyqokeedyqokedyqoke (3 occurrences)
- ysolkeedyqokeedyqoke
- okeedyqokeedyolkeedy
- edyqokeedyqopchedyqok
- eedyqolchedyqokeeyqoke
- qokeedyqotedyqokeedy
- Shedyqokalchedyqokaiin
- edytedyolSheedyqokeey
- edyqokaiinolkeedyqok
- keedyqokeedycheyqokee
- eedyokainchedychedytee
We see a lot of alternation here between ee and e, which we can analyze as substituting the second option k>e within k>e+. If we disregard this alternation in quantities of e, we’re left with the points of departure from the loop which I’ve highlighted below in red, with brackets indicating a “dropped” glyph.
- olchedyqokainolShe[d]yqokain
- okaiinShedyqokeedyqotedy
- edyqokaiinchedyqokeedyl
- edyqokeedycheedyqokeed
- edyqotedyqokeedyqokee
- ealqokeedyqokeedyqoke
- olShedyqokedyqokeedyqo
- ysolkeedyqokeedyqoke
- okeedyqokeedy[q]olkeedy
- edyqokeedyqopchedyqok
- eedyqolchedyqokee[d]yqoke
- qokeedyqotedyqokeedy
- Shedyqokalchedyqokaiin
- edytedy[q]olSheedyqokee[d]y
- edyqokaiinolkeedyqok
- keedyqokeedyche[d]yqokee
- eedy[q]okainchedychedytee
In these examples, we can spot a number of apparent substitutions for smaller or larger stretches of the default qokeedy glyph sequence. Each case can be explained by just one or two less-probable transitions, as follows.
For o_k_ee:
- o_lk_ee, takes second option o>l.
- o_t_ee, takes third option o>t.
- o_pch_ee, takes sixth option o>p (2.88%).
- o_lch_ee, takes second option o>l, then second option l>ch (19.73%).
- o_lSh_ee, takes second option o>l, then fourth option l>Sh (10.72%).
For y_q_o:
- y_o, takes second option y>o.
- y_s_o, takes tenth option y>s (2.16%), then second option s>o (26.53%).
For ee_d_y:
- ee_y, takes third option ee>y.
For y_qok_ee:
- y_ch_ee, takes third option y>ch.
For k_eedyq_o:
- k_ain_o, takes second option k>a; then regular a>i+ but second option within that, a>i.
For k_ee or k_eedyqok_ee:
- k_aiinch_e, takes second option k>a, then first options a>ii>n, then second option n>ch.
- k_aiinSh_e, takes second option k>a, then first options a>ii>n, then third option n>Sh.
The ways in which these longer sequences diverge from the qokeedy sequence may look rather random at first glance, but each can be shown to represent the unfolding of just one or two less-probable transition choices (and wherever there are two, the second might turn out on further analysis to be a consequence of the first—but we’re not there yet).
Of course, there’s a big chunk of the manuscript we haven’t yet considered. When we calculate an equivalent set of transitional probability matrices for Currier A, many of the first options turn out to be different (these cases are marked below with asterisks). Blue and red color-coding is applied as before, except that I’ve lowered the threshold for ambiguity to at least twenty cases going either way because of lower overall counts in this “language.”
- a>i+ (51.96%), a>l (19.37%)
- cFh>y (28.95%), cFh>o (26.32%)
- *ch>o (45.67%), ch>e+ (25.10%)
- cKh>y (34.80%), cKh>e+ (31.35%)
- *cPh>o (33.94%), cPh>e+ (28.44%)
- *cTh>o (38.27%), cTh>y (30.38%)
- *d>a (50.40%), d>y (26.73%)
- *e>o (51.92%), e>y (28.65%)
- *ee>y (51.82%), ee>o (28.24%)
- eee>y (43.02%), eee>s (26.74%)
- f>ch (44.44%), f>o (26.26%)
- g>o (35.29%), g>ch (17.65%)
- i>n (56.09%), i>r (26.21%)
- ii>n (94.80%), ii>r (2.81%)
- iii>n (90.91%), then single instances of iii>r, iii>l, iii>t, iii>d
- k>e+ (30.43%), k>ch (19.59%)
- *l>d (21.92%), l>ch (20.34%)
- *m>ch (23.49%), m>o (20.48%)
- *n>ch (21.25%), n>o (18.16%)
- *o>l (24.99%), o>k (16.53%)
- p>ch (51.23%), p>o (20.70%)
- q>o (97.11%), q>k (1.40%)
- *r>ch (24.82%), r>o (20.35%)
- *s>o (27.92%), s>a (23.38%)
- *Sh>o (46.61%), Sh>e+ (32.49%)
- *t>ch (30.87%), t>o (22.01%)
- *y>d (16.01%), y>ch (15.87%)
Contrastive bigram frequencies have long been used to distinguish Currier A from Currier B, but investigating transitional probabilities rather than absolute quantities may offer a productive alternative perspective on the differences between the two “languages.” For example, if we graphically compare the transitional probability matrices for e, ee, and eee—which seem to display a kind of continuous mutual trajectory as a “series”—we can see the vastly greater probability of a transition to d in Currier B play itself out in the context of other, competing transitional probabilities. This view complements the usual observation that the bigram ed is much more common in Currier B than Currier A.
Perhaps the most striking overall systemic difference we find with Currier A, though, is that instead of a qokeedy loop, there’s another, different closed loop:
- ch>o (45.67%)
- o>l (24.99%)
- l>d (21.92%)
- d>a (50.40%)
- a>i+ (51.96%)
- more specifically a>ii (39.24%; 75.52% within a>i+)
- ii>n (94.80%)
- n>ch (21.25%)
This default loop would generate the sequence choldaiincholdaiincholdaiin, which contains a strong breakpoint at n>ch, plus an ambivalent breakpoint at l>d, and so would predictably appear broken up into words either as choldaiin.choldaiin.choldaiin or chol.daiin.chol.daiin.chol.daiin. We could also express the same prediction as chol,daiin.chol,daiin.chol,daiin, using the convention of “comma breaks.”
Like the qokeedy loop, the choldaiin loop more readily permits escape at certain points than others. Here are the options we encounter while passing through the loop with at least a 10% probability.
- ch>o (45.67%); second option = ch>e+ (25.10%); third option = ch>y (14.69%)
- o>l (24.99%); second option = o>k (16.53%); third option = o>r (16.28%); fourth option = o>d (11.95%); fifth option = o>t (10.61%)
- l>d (21.92%); second option = l>ch (20.34%); third option = l>o (15.49%)
- d>a (50.40%); second option = d>y (26.73%)
- a>i+ (51.96%); second option = a>l (19.37%); third option = a>r (18.34%)
- more specifically a>ii (39.24%; 75.52% within a>i+); second option = a>i (11.87%; 22.84% within a>i+)
- ii>n (94.80%)
- n>ch (21.25%); second option = n>o (18.16%); third option = n>d (15.06%)
As with the qokeedy loop, by choosing single less-probable transitions we can generate familiar-looking sequences such as chor,chol,daiin, chy,daiin,chol, and cheol,daiin.
Torsten Timm has observed that the frequency of words in the Voynich Manuscript has an inverse correlation with the edit distance from three specific words: daiin, ol, and chedy. That is, the more similar to one of these three words another word is, the more frequently it tends to occur. He accordingly groups words into a daiin series, an ol series, and a chedy series based on which word each most resembles. If a word resembles two of these words, he finds that it tends to be even more common than if it resembles only one.
The three series in Timm’s model coincide closely with the two closed loops identified above. Timm assigns chol to the ol series, such that the chol and daiin series could be considered the two “halves” of the choldaiin loop. Meanwhile, he assigns qokeedy to the chedy series, such that the chedy series and the qokeedy loop appear to coincide as well.
One point that should give us pause for reflection is that the most common word Timm identifies in each series—daiin, ol, chedy—doesn’t always match the loop predicted by glyph affinities. There’s no discrepancy with daiin. But how might we account for Timm’s finding that there are 537 tokens of ol to 396 of chol, or that there are 501 tokens of chedy to 305 of qokeedy? The answer could lie in the fact that Timm is analyzing discrete words separated by spaces, while we’re instead analyzing glyph sequences continuously throughout lines. From the latter perspective, ol and chedy will often be fragments of longer sequences that differ from one another, such as rol and yol or lchedy and rchedy, but that end up excluded from the pool of words through frequent spacing as r.ol and y.ol or l.chedy and r.chedy, thanks to the presence of ambivalent breakpoints. By contrast, the sequence qokeedy has no ambivalent breakpoints, and the sequence chol has only the very weakly ambivalent o_l (I count fifteen tokens of cho.l and eleven of cho,l). Thus, I’m inclined to suspect that the higher frequencies Timm found for ol and chedy are, from the standpoint of glyph sequences per se, probably artifacts of spacing. A further circumstantial point in favor of privileging daiin, chol, and qokeedy is that these are the words in each of Timm’s three series with the highest quantities of adjacent exact repetitions:
- .daiin.daiin. (13)
- .chol.chol. (23) versus .ol.ol. (4)
- .qokeedy.qokeedy. (19) versus .chedy.chedy. (7)
Given the overlap between Timm’s series and my loops, it seems likely that Timm’s observations about edit distance from the daiin, ol, and chedy series would also apply to edit distance from the qokeedy and choldaiin loops. If so, then the frequencies of glyph sequences in the Voynich Manuscript would correlate with their adherence to the sequences generated by these two loops, with sequences that deviate less from them being more common, and with sequences that deviate more from them being less common. And if edit distance reckoned in Levenshteinian terms is also comparable in effect to choosing less-probable transitions (which I’ll admit isn’t guaranteed), that would suggest in turn that we’d be able to predict word frequencies based purely on a combination of transitional probabilities and spacing rules. I haven’t tested this hypothesis empirically, but it strikes me as a plausible extrapolation from Timm’s findings.
Moreover, if adherence to the qokeedy and choldaiin loops is a reliable predictor of the frequencies of glyph sequences, that would further support a model in which the default tendency of the script really is to repeat in an endless loop. Of course, much of the text doesn’t repeat conspicuously. When it doesn’t, the incidence of less-probable glyph adjacencies—or, if you will, the entropy relative to the loops—would seem to have risen above some hard-to-define threshold. But whenever such entropy drops below that threshold, we see default adjacencies come to the fore and yield repetitive-looking strings along the lines of qokeedy.qokedy, chor.chol, and daiin.dain. This latter behavior reminds me of nothing so much as an unmodulated carrier in telecommunications—or a minimally modulated one.
Now, as I admitted earlier, the first-order Markov model I’ve been describing may be a bit too simple. If we work out transitional probability matrices for whole bigrams rather than individual glyphs—for example, examining the glyphs that follow after ta rather than just a—we find that the first glyph of the bigram can sometimes make a big difference. In both Currier A and Currier B, for example, the transitions o>k and o>t overwhelmingly dominate after q, y, and n, but they’re less common than o>l, o>r, and o>d after most other glyphs. In Currier B, a transition from a glyph to y appears to be more probable if that glyph is preceded by e+. Such “exceptions” plainly demand attention.
And yet the closed qokeedy and choldaiin loops persist even if we advance to a second-order Markov analysis—that is, working out probabilities for the next glyph on the basis of two preceding glyphs rather than just one. If we start at qo in Currier B, and follow all the first options, we get:
- qo>k (61.91%)
- ok>e+ (43.85%)
- specifically ok>ee (23.69%; 54.03% within ok>e+)
- kee>d (45.10%)
- eed>y (86.55%)
- dy>q (35.55%)
- yq>o (97.88%)
If we start at cho in Currier A, we get:
- cho>l (31.05%)
- ol>d (22.15%)
- ld>a (54.22%)
- da>i+ (65.46%)
- specifically da>ii (49.37%; 75.42% within da>i+)
- aii>n (95.30%)
- iin>ch (20.94%)
- nch>o (44.41%)
And as before, if we start somewhere outside the prevailing loop, we still find ourselves drawn inexorably into it. If we start at qo in Currier A, and follow all the first options, we get:
- qo>k (48.13%)
- ok>e+ (32.53%)
- specifically ok>e (19.43%; 59.73% within ok>e+)
- ke>o (68.92%)
- eo>l (34.07%)
- ol>d (22.15%) — back in the choldaiin loop (via qokeol,daiin.chol,daiin….)
And if we start at cho in Currier B, and follow all the first options, we get:
- cho>l (34.27%)
- ol>k (22.62%)
- lk>e+ (46.37%)
- specifically lk>ee (27.01%; 58.25% within lk>e+)
- kee>d (45.10%) — back in the qokeedy loop (via chol,keedy.qokeedy…..)
The first-order Markov analysis laid out above might not be sensitive to all the nuanced patterns of Voynichese “word grammar,” but it does appear to capture some important patterning that holds up with higher-order analysis, and it has the practical advantage of simplicity. On those grounds, I’m going to stick with it for the moment in the interest of making my investigation of some further complicating factors more manageable.
One final point before I proceed. Some readers may be skeptical that mere transitional probabilities combined with spacing rules could produce the intuitively recognizable “word structure” of Voynichese. As a test, I’ve taken some of my calculated probability matrices and used them as a basis for generating random sequences in turn. Matrices derived from first-order Markov analysis seem to yield an implausibly high proportion of words containing more than one gallows glyph, as in this sequence based on matrices from Currier B:
qol.dy.dor.ol.Shey.or.Shokaiin.Shotalkar.chedy.Shy.chopcholkedy.Sheokeey.s.chcKhdy.chy.okeor.
odytey.odytodain.SheotShey.pchdy.keedy.dal.Shdy.Shetaiin.ol.ol.ody.dytchedy.qol.ol.Shekeedain.
Shedy.qol.l.chedy.dytar.olal.dy.qotey.qosal.cheokaiin.y.otchokchokeedain.cheey.y.pcholkar.Shar.
cheeotchedy.keedar.ain.cheeyty.Sheey.ol.chcKhoteey.l.dy.kaiin
When I use matrices from a second-order Markov analysis, though, I find my results beginning to match the expected structures and rhythms somewhat better. The following example is again based on matrices from Currier B.
ol.qokeodar.ar.okaiin.Shkchedy.Shdal.qotam.ytol.dal.cheokeedy.chkal.Shedy.qokair.odain.al.ol.daiin.
cheal.qokeeey.lkain.chcPhedy.kchdy.cheey.otar.cheor.aiin.Shedy.dal.dochey.opchol.okchy.Sheoar.ol.
oeey.otcheol.dy.chShy.lkar.ain.okchedy.l.chkedy.oteedar.ShecKhey.okaiin.chor.olteodar.okal.qokeShedy.
ol.ol.Sheey.kain.cheky.chey.chol.chedy
Although I generated these sample sequences randomly, I don’t mean to put them forward as evidence that the text of the Voynich Manuscript isn’t meaningful. Rather, I only want to suggest that Voynichese “word structure” could arise as a natural byproduct of transitional probabilities, and that it might be just as compatible with a continuous mode of encoding, glyph by glyph or bigram by bigram, as it is with one that operates on discrete words.
§ 2
Macroscale Analysis
The analysis I’ve presented so far has assumed that transitional probabilities are uniform throughout the text, except for the differences between Currier A and Currier B. But they’re not.
On one hand, there are more granular distinctions that can be drawn among sections of the manuscript. As I’ve mentioned, Quires 13 and 20 already seem to fit certain tentative predictions I’ve made for Currier B better than Currier B text does as a whole. I agree with others that the two “languages,” far from being neatly separable, are better understood as occupying regions of a spectrum. When it comes to developing the ideas I put forward in the previous section, I suspect the first impulse of many Voynichologists would be to investigate transitional probabilities within specific quires or other narrower groupings of folios that are recognized as sharing more than the usual share of features in common. That would certainly be worth doing. I can say, for a start, that Quires 1-3 (a contiguous block of “Herbal A”) independently display the choldaiin loop, while Quires 13 and 20 (two different blocks of Currier B) both independently display the qokeedy loop. By contrast, Quire 19 (a block of “Pharma A”) displays a weaker ol loop into which all other glyphs tend to be drawn, but from which escape is also very likely:
- o>l (32.98%)
- l>o (20.63%)
If we were to discard the analytical distinction between the Currier A and Currier B “languages,” as has been discussed, we might do worse than to substitute Choldaiinese, Qokeedyese, Olese, and maybe other loop-defined groupings yet to be discovered—perhaps with more nuanced subdialects of each.
But transitional probabilities—and other related features—also vary by position both within lines and within paragraphs. I’ve taken to calling the two parameters in question rightwardness and downwardness, such that phenomena can be more leftward or rightward in lines and more upward or downward in paragraphs. It’s this other kind of variation I’d like to explore here next.
A few positionally variable factors have long been recognized. For example, the probability that the first glyph in a paragraph will be p is extremely high (around 45%), and p and f appear far more often in the first lines of paragraphs than anywhere else. Similarly, m and g appear far more commonly as the last glyph in a line than in any other position. Like “word structure,” these last-mentioned patterns are easy to spot even through casual browsing. From the standpoint of “word grammars,” such phenomena are typically regarded as exceptions, prompting such questions as whether the first words of paragraphs are “normal” words with p prefixed to them. But if we shift our focus away from words and towards continuous glyph sequences, these patterns can be seen as entirely regular—just with respect to a different, larger-scale frame of reference.
To accommodate the issue of positional variability, I’ve experimented with defining different quantities of positional category within lines, such as these—
- A: The first adjacency in the line
- B: The first third of the line (excluding first and last adjacencies)
- C: The middle third of the line (excluding first and last adjacencies)
- D: The last third of the line (excluding first and last adjacencies)
- E: The last adjacency in the line
—and also different quantities of category by paragraph position, such as these:
- 1: The first line of the paragraph
- 2: The remainder of the first half of the paragraph
- 3: The second half of the paragraph, excepting
- 4: The last line of the paragraph
A framework of this sort enables us to compare and contrast phenomena of interest within each of the combinations of line position and paragraph position (e.g., A-1, A-2, A-3, A-4, B-1, B-2, B-3, B-4, etc.) as well as for each of the line positions for all paragraph positions (e.g., A:E-1, A:E-2, etc.) and each of the paragraph positions for all line positions (e.g., A-1:4, B-1:4, etc.). It maps information onto a grid like the following one, in which squares in columns A and E and rows 1 and 4 are especially likely to represent sets of unlike size from the others.
I’m unsure what the optimal number of divisions is for lines and paragraphs. Is it best to divide the line into three parts, as here, or into four quarters, or five fifths, or seven sevenths? Would it be better to divide the paragraph into three thirds than into two halves, so that we could assess the “middle” third? The main advantage of increasing the number of divisions is enhanced precision and a greater ability to distinguish continuous trends. The main disadvantage is the reduction of the available dataset within each division, which amplifies the effects of random noise. There’s probably a sweet spot to be found here through trial and error, and this may become more clear over time than it is right now.
One of the simplest things to track in this way is glyph distribution: all we need to do is count the glyphs in each section of the line. I designed my script mainly with transitions between glyphs in mind, though, so it divides the line into segments in terms of those, as described above, rather than in terms of the glyphs themselves. When it comes to counting the first glyphs of bigrams, which are my primary point of reference, the first segment of the line contains the first glyph of the line (preceding the first transition), the last segment of the line contains the second-to-last glyph of the line (preceding the last transition), the other groups represent fractions of the stretch from the second glyph through the third-to-last glyph, and the last glyph of the line isn’t tracked at all. However, I also keep an extra count of the second glyphs of the bigrams—the glyphs that are transitioned to—so by analyzing those as well, we can regain the lost symmetry.
As I mentioned above, it has long been known that the distribution of some glyphs varies by position. The observation that certain glyphs are disproportionately rare or common at the beginnings or ends of lines, or disproportionately common in the first lines of paragraphs, dates back to Prescott Currier:
The frequency counts of the beginnings and endings of lines are markedly different from the counts of the same characters internally. There are, for instance, some characters that may not occur initially in a line. There are others whose occurrence as the initial syllable of the first ‘‘word’’ of a line is about one hundredth of the expected…. There is…one symbol that, while it does occur elsewhere, occurs at the end of the last ‘‘words’’ of lines 85% of the time…. [The symbols p and f] appear 90-95% of the time in the first lines of paragraphs, in some 400 occurrences in one section of the manuscript.
Patterns such as Currier mentioned could perhaps be explained in terms of superficial tweaks to text that is otherwise uniform in character: elaborating t and k into p and f in the first lines of paragraphs, extending n into m at the ends of lines, and so on. However, I believe evidence has been mounting that glyphs can also display continuously variable distribution throughout lines and paragraphs, which makes the variation rather harder to segregate neatly from the rest of one’s analysis. Here’s a graph I posted to the Voynich.Ninja forum showing counts for some common glyphs in each of five “internal” line positions based on the line-division strategy described above—my first crude attempt at plotting data of this kind.
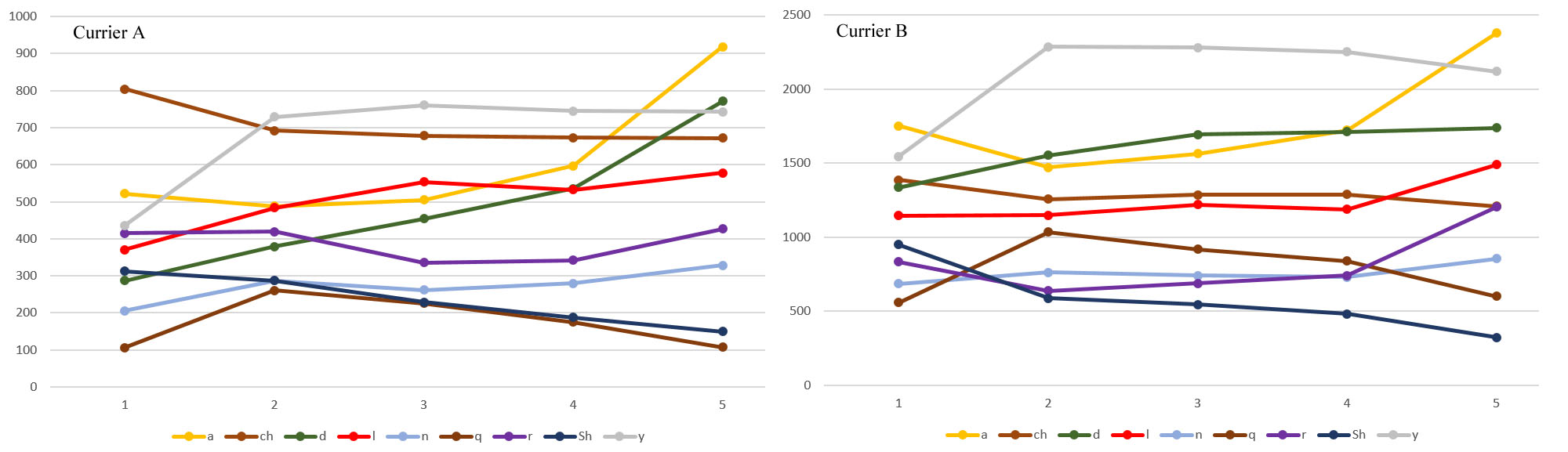
Here are a few of the specific sets of five numbers from the same dataset for Currier A:
- s: 92, 134, 139, 185, 204
- ch: 804, 692, 678, 673, 672
- Sh: 312, 287, 229, 187, 149
- d: 287, 379, 454, 536, 771
Even without a graph, it’s easy to see here that the counts for s and d go continuously up, while the counts for ch and Sh go continuously down, and that the rates of change also differ from case to case.
My first impulse was to calculate single rightwardness and downwardness “scores” for glyphs, bigrams, words, and such to reflect their overall average inclinations rightward or leftward and upward or downward. But I’ve since tried applying some more elaborate visualization strategies to this kind of data, and it’s becoming increasingly apparent that the distribution of many Voynichese glyphs varies according to patterns that have shapes as well as directions.
Here’s one technique I’ve been using. I divide paragraphs into five sectors—1 = first line, 5 = last line, and 2-4 = whatever remains in the middle, divided into thirds—and I simultaneously divide lines into fifths (for a first analysis) and sevenths (for a second analysis), both times splitting off the first and last adjacencies as well. This arrangement maps positions onto a 2D grid along the lines laid about above, 5×7 in the one case, 5×9 in the other. For each of the eighty groupings that result, I tally the first glyphs and second glyphs of each adjacent glyph pair. This may seem like a clunky approach, but by combining the two counts I can get totals for all glyph tokens in first position, second position, last position, and second-to-last position, as well as a pair of totals for each intermediate group with their “windows” offset by just one position. Finally, I divide each result by the total count in its cell of the grid to normalize the figures for group size. Then it’s time to take a look at what we’ve found. On the left of my display, I plot the results for the first two positions; on the right, the results for the last two positions; and in the middle the results for all the intermediate positions, with the fifths and sevenths interleaved, and with the results of the “first glyph” and “second glyph” counts offset by a slight, arbitrary distance along the x axis. Each of the four interleaved series of plot points (first glyph with five divisions, second glyph with five divisions, first glyph with seven divisions, second glyph with seven divisions) is connected by a separate line. On top, I show the results for each separate paragraph sector color-coded in a way that’s meant to suggest a blue-to-red spectrum: (1) dark blue for first lines, (2) light blue for first thirds, (3) gray for second thirds, (4) yellow-orange for last thirds, and (5) red for last lines. On the bottom, in green, I show the aggregate values for all paragraph sectors lumped together.
With all that explanation out of the way, let’s look at some results.
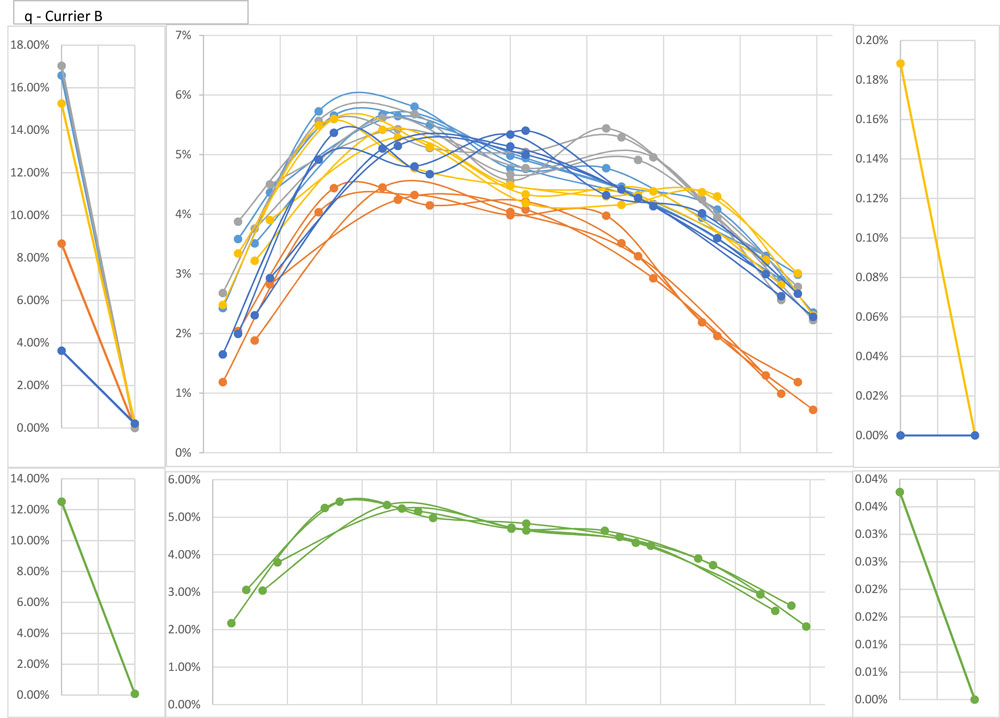
A good example of a glyph with a distinctly-shaped distribution is q. Here’s a display of data for it from Currier B, showing a characteristic double hump with a higher peak on the left. The color-coding may be more challenging to take in visually than the curve-shape is, but the red (last lines) and dark blue (first lines) sort lower than everything in the middle; the average percentages for the five paragraph sectors are 3.87, 4.55, 4.62, 4.32, and 3.09. Thus, q seems to gravitate towards the middle—or to shy away from the extremities—in both lines and paragraphs.
Such convergent tendencies within lines and paragraphs don’t seem to be the rule, but another possible case is the distribution of Sh in Currier A. The aggregate (green) curve below shows a clear downward slope in prevalence across lines, from around 4.5% to around 1.5%. Meanwhile, the color-coding indicates that Sh is more prevalent in the first lines of paragraphs (dark blue), and less prevalent in the last lines of paragraphs (red), than anywhere else. It’s true that the downward trajectory isn’t wholly consistent in between (average percentages for sectors are 4.81, 2.74, 2.61, 3.03, 2.13), but for the most part, it seems that Sh becomes less common the further we go along in a line or in a paragraph, rightward and downward.

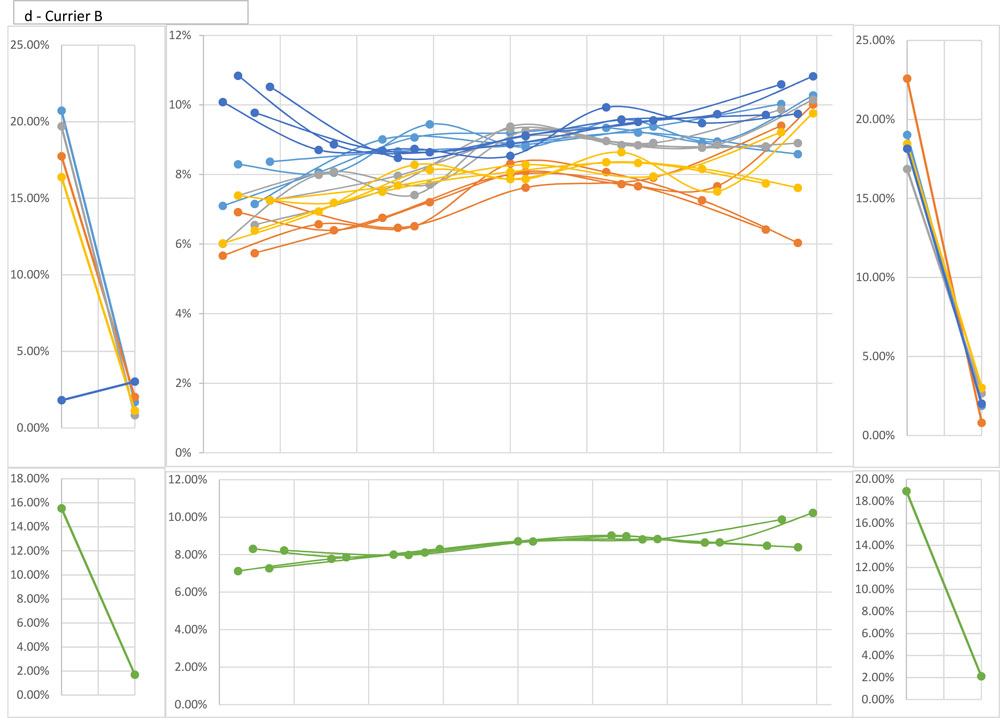
Here’s a similar graph for d in Currier B. This time, the aggregate (green) curve shows comparatively little variation within lines, but prevalence decreases with striking consistency across paragraphs; average percentages for the five sectors are 9.34, 9.18, 8.72, 8.13, and 7.93.
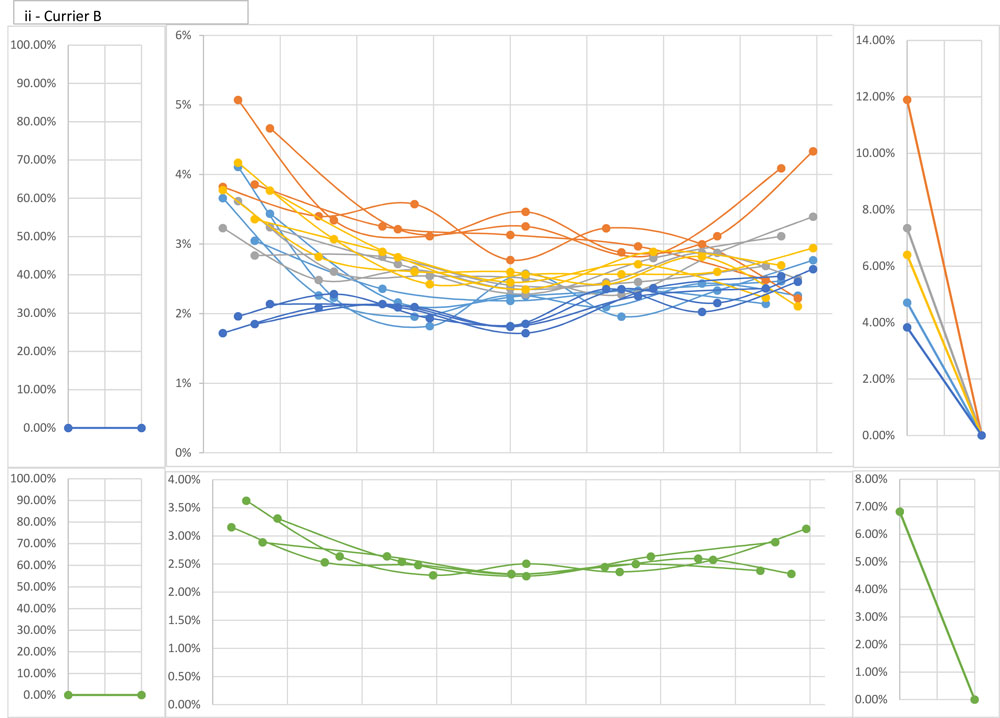
Meanwhile, ii shows the exact opposite trajectory in Currier B; average percentages for the five paragraph sectors are 2.08, 2.40, 2.69, 2.74, and 3.33. The pattern for i is similar (average percentages 1.70, 1.87, 1.93, 2.07, 2.28) but harder to make out visually because of the smaller differences, so that I overlooked it at first. For what it’s worth, neither pattern is evident in Currier A.
Those are just a few out of many similar graphs I could have chosen. Most glyph types turn out to have their own unique patterns of distribution within whole lines and paragraphs, just as surely as they prefer to be adjacent to certain other glyph types. While this phenomenon has only just started to be recognized and investigated, it’s one with which I suspect any theory about how the Voynich Manuscript works will ultimately need to come to terms.
One response to this widescale positional variability would be to posit that there are separate microscale and macroscale factors at play in the structure of Voynichese. By microscale factors, I mean the ones that govern the level of transitions between individual glyphs. The conspicuous formal regularity on this level has inspired many studies of “word structure,” as well as my own line of speculation above regarding the qokeedy and choldaiin loops, and the relevant rules for valid words seem, at least on the surface, to apply fairly uniformly. By contrast, macroscale factors would concern the preferential, non-uniform ways in which glyphs are distributed with respect to whole lines and paragraphs. If microscale analysis addresses the question of why the glyph y appears in one particular place in one particular word, macroscale analysis might instead address the question of why it appears where it does on the page.
It might seem at first glance as though a wide gulf separates those two levels of analysis, with no clear path to get from the one to the other. But I think the approach I began developing in the preceding section could help us bridge them, at least as far as the mechanics of analysis go. If the distribution of a glyph varies by position, the aggregate probabilities of transition to that same glyph must necessarily also vary by position—there’s no way, statistically, that it could be otherwise. To accommodate that reality, we could simply qualify our transition probability matrices to stipulate that the probability of, say, l>d isn’t uniform for all line positions but varies as a function of them, so that the macroscale dynamics are integrated into the microscale dynamics, and vice versa.
I’ll admit that “simply” may be a bad choice of word; this is a conceptually simple step, but not necessarily simple to put into practice. (Jorge Stolfi’s “word grammar” could perhaps be adapted similarly by adding one or more positional dimensions to his frequency statistics, if anyone would like to try.) I’ll also admit that this arrangement, in itself, can’t explain anything. It only provides a mechanism for organizing statistical data so that we can look for patterns in it. What those patterns might mean is another matter entirely.
By way of a start, let’s take a look at how positional variability impacts the two closed loops that emerged from our earlier analysis: the choldaiin loop in Currier A and the qokeedy loop in Currier B. Whatever conclusions we might end up drawing about the loops as such, I believe it’s fair to treat them as representative test cases for the microscale structure of Voynichese. I can’t imagine how any factor powerful enough to disrupt them wouldn’t also disrupt the structure as a whole, regardless of whether we analyze it through transitional probability matrices or a “word grammar” such as Stolfi’s.
The two weakest links in the choldaiin loop are l>d (21.92%) and n>ch (21.25%), and if we look at these transitions within Currier A more closely, we discover that each of them actually dominates only in a certain limited part of the line. For most line positions, it turns out that l>ch is actually more probable, but at the very end of the line, l>d becomes so overwhelmingly strong as to tip the overall statistics for the whole line in its favor. The following graphs exclude the first and last transitions of lines to let us focus on the “internal” situation.
Meanwhile, n>ch dominates through much of the early-to-middle part of the line, but n>o is more probable right at the beginning and—as n>ch starts to decline—becomes more competitive again, while n>d rises steeply to overtake both towards the very end.
Since the line segments in which l>d and n>ch dominate don’t significantly overlap, there doesn’t actually seem to be anywhere the choldaiin loop as a whole would pertain. This loop turns out to be even more of an abstraction than I’d thought. The first half of the line would hypothetically loop chol,chol,chol by default, while the last third of the line would loop daiin.daiin.daiin. On that basis, it might be more defensible to think in terms of separate chol and daiin loops that can either repeat independently or alternate with each other (which would end up conveniently mirroring Timm’s identification of separate ol and daiin series of words).
If we compare the major Currier A transitions for l and n by paragraph sector rather than by line position, we find variation on that front as well.
On the left, we see that l>d holds an early lead and maintains its absolute level fairly steadily, but that l>ch rises to overtake it by the middle third of the paragraph. On the right, we see that n>o dominates the first lines of paragraphs, but that n>ch dominates everywhere else, and more strongly the further downward in a paragraph we go. The transitions l>Sh and n>Sh turn out to be especially strong in the first lines of paragraphs as well, and to decline in what looks like inverse proportion to the rise of l>ch and n>Sh. Thus, the constituent probabilities of the choldaiin loop vary by position within paragraphs as well as within lines. Curiously, n>ch and l>ch both become less dominant as we move rightward in lines but more dominant as we move downward in paragraphs. In other words, they don’t show any one trajectory as we move “forward” in the text, but two mutually contradictory ones.
The next weakest link in the choldaiin loop after l>d and n>ch is o>l (24.99%), but it turns out to be a lot more resilient with regard to positional variation. It consistently maintains its first-place status across all line positions, although its distance from o>r and other competitors varies.
The situation is similar with variation by paragraph sector: there are some notable differences among transitional probabilities from o, such as the unusually low proportion of o>k in the first lines of paragraphs, but o>l holds its lead everywhere.
You may recall that Quire 19 (“Pharma A”), analyzed as a whole without factoring in positional variation, displays an ol loop rather than a choldaiin loop. The only refinement in the general characteristics of Currier A needed to bring that about would be an increase in the probability of l>o relative to l>ch and l>d—an exaggeration, perhaps, of the relative trajectories we see in the middle of the line, where l>o is most competitive. We would then have Olese rather than Choldaiinese.
How about the qokeedy loop? Every one of its links is stronger than l>d, n>ch, and o>l in the choldaiin loop. However, its weakest two links are y>q (28.11%) and o>k (30.31%), so let’s take a quick look at those. First, y>q is consistently dominant throughout the line in Currier B, even if y>o begins to approach it in probability towards the very end.
Meanwhile, o>k dominates every position except for the very beginning, where o>l has a slight edge over it.
 There’s also some variation by paragraph position in these same transitions from y and o, particularly in the first and last lines, but we don’t see the complex crossovers we did for transitions from l and n in Currier A.
There’s also some variation by paragraph position in these same transitions from y and o, particularly in the first and last lines, but we don’t see the complex crossovers we did for transitions from l and n in Currier A.
On the whole, the qokeedy loop seems to pertain more consistently in Currier B than the choldaiin loop does in Currier A.
Unsurprisingly, the patterns of transitional probability we’ve been examining bear at least some passing resemblance to the patterns of distribution of the individual glyphs the transitions are to. We know, after all, that these phenomena must relate to each other somehow. But it’s worth asking just how closely the two patterns resemble each other. The answer seems to vary from case to case.
Consider l>d in Currier A: its rise to dominance late in the line coincides with a jump there in the proportion of total glyphs made up by d itself. In other words, l>d becomes more probable as d becomes more common. Meanwhile, l>ch also becomes less probable as ch becomes less common. If we divide the line into five analytical segments and plot the probability of l>d against the proportion of second glyphs that are d, and the probability of l>ch against the proportion of second glyphs that are ch, we find that the resulting plots come out impressively straight, just as we’d expect from a close linear correlation.
The gradients both look to be in the ballpark of 1:5, which is to say that a 1% change in the overall share of the glyph in the mix seems to correspond to a 5% change in the probability of the relevant transition. Given that Voynichese glyphs prefer so strongly to transition to other specific glyphs, it might not be strange to see a change in glyph distribution have an amplified effect on an associated transitional probability.
If we split the line into seven analytical units instead of five, we turn up more chaotic back-and-forth around positions 4 and 5, right where l>d is overtaking l>ch in probability, but the overall directionality is similar. It’s notable, too, that multiple points cluster closely together: 1, 2, 3 and 4, 5 in the plot for l>d versus d and 2, 3, 5 (but not 4) in the plot for l>ch versus ch, as though the possibilities are somehow quantized and can only jump between discrete values when some kind of tipping point is reached. (This phenomenon was also noticeable to a lesser degree with just five line divisions: note the apparent clustering above of positions 1 and 2 for both l>d and l>ch, and of positions 3 and 4 for l>ch.)
But other cases aren’t as tidy as this one. For n>ch, we’d need to make a three-way comparison with both n>o and n>d, and o, you may recall, is one of those glyphs we know isn’t handled well by our first-order Markov analysis in the first place. Here’s what we find:
My graph’s y axis is more compressed this time than before, so the gradients are actually more similar than they look to those we saw above. And if we consider just the displacement between line positions 1 and 5, the change in the transitions is roughly what we’d expect from the change in frequency of the associated glyphs. Points 1, 2, and 3 for n>d and n>o, and points 1 and 2 for n>ch, also seem to show the same “clustering” phenomenon we observed earlier. But we don’t quite see the steady, progressive slope we see when we plot l>d against d. Of course, we’re only considering rightwardness here, and not downwardness; maybe taking the two together would help. But it looks as though variation in transitional probabilities might not always just recapitulate overall variations in the distribution of individual glyphs. At least, I can’t reliably predict the one from the other to my satisfaction just yet.
Still, I believe it’s at least safe to say that positional constraints work on smaller units of text than words, regardless of whether those smaller units prove specifically to be glyphs or transitions or bigrams or some combination thereof. Since positional tendencies implicate such granular details as whether n is more likely to transition to ch, d, or o, or how likely d is to occur in general, they must plainly be operating at the sub-word level. To the extent that words also show patterns of variable distribution by position, that’s presumably because they’re built up from the results of smaller-scale processes on which positional factors exert a more direct influence.
Let’s next examine a few transitions from a slightly different angle, using a display more like the one I used earlier for examining glyph distributions. (Just getting a good look at what’s going on often feels like half the battle!) The graphs below show transitional probabilities for o>t, o>k, l>y, and d>y color-coded by paragraph sector as before, with line positions assigned to the x axis (1=first transition, 9=last transition, and 2-8=seven intermediary segments), and with statistics for Currier A on the top and Currier B on the bottom.
There’s plenty to see here, but for the moment I’d like to draw out just a few specific observations. First, o>k is less probable in the first lines of paragraphs—plotted in dark blue—than anywhere else, while o>t tends by contrast to be more probable there than it is overall. Second, o>t and o>k often display conspicuous peaks at the first transition in the line—position “1” on the x axis—though not always. Third, l>y and d>y are both more probable as the last transition in a line than anywhere else, but l>y more extremely so than d>y, and with the discrepancy between the two being greater in Currier B than in Currier A.
The reason I’ve singled out these four specific transitions for consideration here is that they also happen to be characteristic of the most common “label” words—that is, self-standing glyph sequences that occur outside the context of lines and paragraphs. The very existence of labels could perhaps be seen as undermining any line of speculation centered on positioning within larger-scale structures, since labels don’t seem to belong to such structures and might be taken as proof that Voynichese can function perfectly well without them. But only certain specific sequences with a remarkably consistent structure can be found appearing more than three times as labels:
- 8 tokens: otaly, otedy
- 6 tokens: okal, okary, oky
- 5 tokens: okaly, okeody, okol, otchdy
- 4 tokens: okedy, okody, oteedy, otol, otoly
All fourteen of these sequences begin with ot or ok, while nine of them end with ly or dy (r>y, as in okary, is also overwhelmingly more probable at the ends of lines than elsewhere).
Some of these sequences aren’t particularly common in paragraphic text. Disregarding word breaks, I count 5 tokens of otaly in Currier A and 21 in Currier B; of okaly, 17 and 29; of okary, 2 and 12. From the standpoint of “word morphology” and overall word frequencies, then, the frequent appearance of these distinctively-structured words as labels would present something of a mystery.
However, if we consider these label sequences not as words but as unusually short lines, they conform somewhat better to expectations. As we’ve seen, the transitions l>y and d>y are disproportionately common at the ends of lines, just as they are at the ends of these labels. The situation with o>k and o>t is less clear-cut, but both transitions display conspicuous beginning-of-the-line peaks under at least some circumstances, much as they appear conspicuously at the beginnings of these labels. In the context of ordinary lines, o>k or o>t might tend not to appear often in close proximity to l>y or d>y or r>y because a number of middle-of-the-line glyphs usually separate them. But within the smaller compass of a label, the same positional constraints might make their appearance together far more likely. I offer this as one intriguing hint that the same forces that shape the macroscale structures of lines and paragraphs might apply to labels as well.
One more phenomenon that seems to vary by position is spacing. I haven’t analyzed this as thoroughly as I could, although some of my Python scripts distinguish between spaced, unspaced, and comma-spaced variants, in addition to giving the totals of all these, which quadruples the already-bloated size of the spreadsheets. For now, I’ll content myself with sharing statistics for just one of the glyph adjacencies we’ve just been looking at, l_y. The figures below give the token quantity apart, with a comma (i.e., uncertain), and together, and then the “apart” count as a percentage of the “together” count.
- 1st adjacency: unattested
- 1st third of line: Currier A = 14, 2, 20, 70%; Currier B = 15, 3, 13, 115%
- 2nd third of line: Currier A = 26, 0, 42, 62%; Currier B = 26, 5, 53, 49%
- 3rd third of line: Currier A = 17, 2, 50, 34%; Currier B = 18, 2, 51, 35%
- Last adjacency: Currier A = 2, 2, 146, 1.3%; Currier B = 0, 3, 123, 0%
Judging from these figures, the probability of a space being inserted between l and y isn’t uniform but decreases steadily over the course of a line. We might hypothesize that this pattern reflects the writer tending to run out of room towards the ends of lines and trying to cram glyphs together more closely there, but I doubt that’s the cause. In an earlier study I made only of the total average “rightwardness” of spaced and unspaced variants, I found similarly that ly is more rightward on average than l.y is, but that for some other glyph pairs, it’s the spaced variant that’s more rightward on average—that is, a space apparently becomes more likely to be inserted between them the further along in a line they appear. And these differences display distinct patterns of their own, so they don’t seem to represent mere statistical noise.
There’s one more point I should make before moving on. When I look for an aggregate pattern that “should” be more common in one part of a line than another, based on the foregoing analysis, it tends not to be. But the usual entropy of the writing may be great enough overall to “drown out” the effects of the patterns on the level of individual lines and words. That’s not a bad thing. I hold out hope that the entropy will prove to be the meaningful part.
§ 3
Intermediate-Scale Analysis
As I acknowledged earlier, first-order Markov modeling doesn’t accommodate all the detectable patterns of Voynichese. Second-order Markov modeling seems to fare better, and third-order Markov modeling better yet. But the first-order modeling already captures so much of the patterning that ratcheting up our analysis in this direction seems more likely to refine its findings than wholly to overturn them. Transitional probabilities often seem to depend on the single glyph that immediately precedes the transition. If it seems they sometimes don’t, it’s worth looking closely at the “exceptions” to see whether they share any characteristics in common.
It remains an open question, of course, whether the “exceptions” are due to characteristics of the script itself or of content to which the script has been applied. Especially if the text is meaningful, its patterning shouldn’t be entirely predictable. In particular, I don’t believe the goal of a model should be to predict all attested words as valid and to reject all non-attested words as invalid. Given how many words or sequences in the Voynich Manuscript are unique, appearing only once, I’d argue that any plausible model ought also to predict words and sequences that would have been unique if they had appeared—or that might have appeared only on one of its missing pages. In Stolfian terms, it should also predict the occasional word with multiple core letters, multiple coremantles, or other “anomalous” features, since these are demonstrably admissible even if they’re comparatively rare. On this level, first-order Markov modeling might actually be perfectly satisfactory. Where it falls short is in predicting certain relative frequencies: for instance, the ratio between the token quantity of qok and the token quantity of qor. To be fair, that’s not something most “word grammars” tend to be able to do (or to try to do) either. But since the whole transitional-probabilities approach is based on relative frequencies in the first place, its validity might be held to stand or fall on that basis more than the validity of other approaches would.
To study the situation more methodically, I calculated transitional probability matrices for bigrams, as well as for just the second glyphs in the context of bigrams (e.g., or> vs. *r>, where * represents the first glyph in a bigram, excluding line-initial r>). I also made a similar comparison of transitional probability matrices for trigrams with those of their concluding bigrams (e.g., dol> vs. *ol>); and for quadrigrams with those of their concluding trigrams (e.g., doky> vs. *oky>); and similarly for quinquegrams, sexagrams, and septagrams. If needed, I could continue the same process indefinitely, but by the time we hit septagrams, we’ve already reached the length of the qokeedy loop and exceeded the length of the average word.
This approach makes it easy to detect cases in which earlier glyphs appear to correlate more strongly with subsequent transitional probabilities than the glyphs that immediately precede the transitions do. For example, if we focus on Currier B (as I will for the examples that follow until further notice), we find:
- *d>a: 24.57%
- Much less probable: eed>a: 8.15%, ed>a: 11.45%
- Less probable: chd>a: 21.88%, Shd>a: 22.56%
- More probable: od>a: 34.83%
- Much more probable: ld>a: 50.88%, yd>a: 66.88%, nd>a: 72.67%, rd>a: 72.73%
And also:
- *d>y: 66.73%
- Much less probable: nd>y: 11.05%, yd>y: 15.42%, rd>y: 17.05%, ld>y: 37.17%
- Less probable: od>y: 52.42%, Shd>y: 64.02%
- More probable: chd>y: 69.71%
- Much more probable: eeed>y: 83.10%, ed>y: 83.59%, eed>y: 86.55%
It’s evident here that the likelihood of a transition from d to y or a has a strong correlation with the glyph that precedes the d. Overall, the transition d>y is a little more than two and a half times more probable than d>a. However, after n, y, r, and l, d>a is actually more probable than d>y, while after e, ee, and eee, the probability of d>y exceeds that of d>a by much more than usual. This latter shift is also found occurring in transitions from numerous other glyphs: ch>y, cKh>y, cTh>y, k>y, s>y, Sh>y, and t>y all become significantly more probable after e+.
Here’s another pair of related cases:
- *o>r: 8.93%
- Much less probable: qo>r: 0.57%
- Less probable: no>r: 5.16%, yo>r: 5.83%
- More probable: eo>r: 10.91%, eeo>r: 11.73%, ro>r: 13.81%, cho>r: 14.78%
- Much more probable: Sho>r: 17.05%, so>r: 18.56%, to>r: 19.27%, lo>r: 19.57%, ko>r: 22.78%, do>r, 24.82%
And:
- *o>k: 30.43%
- Much less probable: eeo>k: 2.30%, ko>k: 2.85%, to>k: 4.32%, eo>k: 5.42%, so>k: 7.78%, do>k: 7.91%, Sho>k: 9.09%, cho>k: 10.45%
- Less probable: lo>k: 16.81%, ro>k: 19.10%, no>k: 28.91%
- More probable: yo>k: 32.31%
- Much more probable: qo>k: 61.91%
This case resembles the last one: we can see that the glyph that precedes the o strongly affects the likelihood of a transition to r or k afterwards. After q, o>k is overwhelmingly more probable than o>r, and it’s also much more probable after n and y. But after most other glyphs, it’s the other way around: o>r is more probable than o>k. Nor are these isolated cases; *o>t behaves much like *o>k, and *o>l much like *o>r.
Here’s yet another related pair of cases:
- *y>k: 5.90%
- Less probable: dy>k: 2.87%, eey>k: 3.82%
- More probable: ey>k: 6.68%, chy>k: 7.85%
- Much more probable: ly>k: 17.20%, ry>k: 26.67%, ny>k: 38.24%, yy>k: 44.64%
And:
- *y>t: 4.67%
- Less probable: dy>t: 2.41%, eey>t: 2.99%, ey>t: 4.18%
- More probable: chy>t: 5.52%
- Much more probable: ly>t: 11.83%, ry>t: 26.06%, ny>t: 33.53%, yy>t: 35.62%
This time it’s the similarities between the two cases to which I want to draw attention rather than the differences. The glyphs preceding y line up in identical order when ranked according to the probability of a subsequent transition from the y to k or t: namely, d, ee, e, ch, l, r, n, y.
Let’s now consider a few different explanations for why a first-order Markov analysis of Voynichese might fall short in its predictions, and the implications of our findings so far for them.
- Voynichese is encoded continuously in a way consistent with transitional probability matrices, but certain bigrams, such as ok or qo, behave as distinct and inseparable elements rather than as combinations of their parts.
- Voynichese has a significant “word structure” after all, or at least a cyclical structure, such that the probability of k or r following after o varies based on which slot in the cycle o itself fills.
- Voynichese is encoded continuously in a way consistent with transitional probability matrices, but glyphs can sometimes affect transitions beyond the ones that follow immediately after them.
I believe the first of these hypotheses is the least promising of the three based on the patterns we’ve examined so far. The most notable discrepancies have appeared to involve:
- A correlation between y, q, or n and an increased probability of transition to a gallows glyph two positions later.
- A correlation between e+ and an increased probability of transition to y two positions later.
So, for example, when n precedes either y or o, we find that the y or o is more likely in turn to transition either to k or t. If bigrams such as ny or yk were behaving entirely as distinct and inseparable units, rather than as combinations of n+y and y+k, it seems to me that we wouldn’t expect their pieces to display such individually consistent correlations. As it stands, even when the probabilities of transition from one glyph vary greatly depending on the glyph that precedes it, the options still seem to follow fairly set patterns. The first choice after o is usually either k or l, and if it happens to be something else—such as d after eo and eeo—it’s generally still a reasonably high-ranking choice in other cases too.
Hypotheses two and three both seem tenable at this point, but for the moment I’m mainly going to pursue hypothesis number three, in part because it seems more consistent with the path we’ve followed here so far. I believe that one of the strengths of the transitional-probability approach is that it predicts cyclical behaviors—such as the qokeedy loop—without requiring them to be defined a priori as a point of reference. We’ve already seen how much of the basic “word structure” could emerge naturally through the interplay of smaller-scale rules operating on a glyph-by-glyph basis. I’d like to continue looking for models that involve the fewest and simplest rules, and that center on dynamics by which structures could emerge rather than on outlining specific structures as such.
With that in mind, I’d like to propose a theory of delayed influence, beginning with the conjecture that a glyph can exert an influence not only on the transition immediately following it, but on the transition after that as well, complementing the influence of whatever glyph intervenes. According to this theory, after the sequence ny—for example—the effective transitional probability depends partly on the y, with its matrix of probabilities for a glyph that immediately follows, but partly also on the n, with its separate matrix of delayed probabilities for a glyph two positions ahead.
It’s cumbersome to investigate patterns of delayed influence on a case-by-case basis as I’ve been doing, so I’ve made an effort to come up with methods of detecting them more efficiently.
Here’s one approach I’ve tried, which has its weaknesses but still seems useful and informative. For each transition from a given bigram (e.g., ny>k), I count both the occurrences of the specific transition and the quantity of all transitions from that same bigram (e.g. ny), and I also calculate the transitional probability for just the latter half of the bigram (e.g., *y>k, where *y represents a bigram of which y is the second element, excluding line-initial y). I then multiply the transitional probability matrix for the latter half of the bigram (e.g., *y>k) to the count of tokens of the bigram (e.g., ny), thereby yielding a prediction of the number of tokens of the transition (e.g., ny>k) we should expect if the first element in the bigram (e.g., n) had no influence on the transition. There are 170 transitions from ny and 65 occurrences specifically of ny>k, while the probability of *y>k is 5.90%. If the n had no influence on the transition ny>k, and if that transition behaved like *y>k in general, we would expect there to be about 170×0.0590=10.02 occurrences of it, i.e., just over ten. Instead, there are 65—around six and a half times as many as predicted. So far, this just confirms the discrepancy I cited above: ny>k has a probability of 38.24%, about six and a half times the generic probability of *y>k. But I can now also select all transitions of the form n*>k, tally the actual counts and the predicted counts, and compare the sums to see if there’s any significant aggregate difference for the whole set. In doing this, it’s important to include counts of zero for any attested transitions **>k that never appear as n*>k, as well as the non-zero predictions for those same transitions. With that measure in place, I’ve confirmed that the sums of the actual occurrences equal the sums of the predictions, so my algorithm at least seems to be doing what I meant for it to do (which I try never to take for granted).
For n*>k, the sum of all actual occurrences is 500, and the sum of all predictions (rounded to the nearest integer) is 425. Thus, n appears on average to boost the probability of a transition from the glyph that follows immediately after it to k to ~118% of its usual level. However, the magnitude of the boost varies a lot from case to case, and in one instance, no>k, there’s actually a slight decrease.
- nch>k: 31 actual, 13.77 predicted (~225%)
- nSh>k: 13 actual, 6.72 predicted (~193%)
- no>k: 364 actual, 383.10 predicted (~95%)
- ny>k: 65 actual, 10.02 predicted (~649%)
- nl>k: 19 actual, 7.58 predicted (~251%)
One complication may be that the figure for no>k—for example—is included in the figure for *o>k on which the prediction for no>k is based in turn, so that the influence from n could already be contaminating our point of reference. To avoid that, we could always predict a token quantity for no>k based on a probability calculated for all *o>k except no>k. But I’ve tried that “fix,” and the results aren’t much different. And maybe I shouldn’t have expected them to be. After all, a further problem it doesn’t address is that other glyphs, such as y, seem to exert a similar influence to that of n, so that even if we remove all n*>k from our calculation of probabilities for **>k, transitions from bigrams beginning with those other glyphs, such as y*>k, remain and could skew overall results:
- ych>k: 28 actual, 17.4 predicted (~161%)
- ySh>k: 17 actual, 7.97 predicted (~213%)
- yo>k: 632 actual, 595.18 predicted (~106%)
- yy>k: 104 actual, 13.74 predicted (~757%)
- yl>k: 254 actual, 160.25 predicted (~159%)
Meanwhile, other glyphs inserted into *y>k, *ch>k, *o>k, and so forth might tug the overall results in the opposite direction, with each case having an influence proportional to the commonness of its bigram. I’m sure that part of the reason why yy>k and ny>k exceed their predicted counts so dramatically is that an even more common combination brings down the average probability for *y>k with respect to which the predictions were made.
- dy>k: 150 actual, 307.88 predicted (~49%)
By contrast, the equivalent transition for *o>k is relatively uncommon, which helps account for the fact that yo>k and no>k come so much closer to the predictions based on overall averages in that case, while the other transition deviates even more from its prediction.
- do>k: 22 actual, 84.59 predicted (~26%)
Thus, many disparate factors are likely to be playing into each of these figures. I’m not sure there’s any “pure” point of reference for a transition such as *o>k that’s truly neutral with regard to preceding glyphs; and without one, the method I’ve described is bound to be at least somewhat inaccurate even if the hypothesis in which it’s rooted is correct. As it stands, some of the individual results for a set such as y*>k or n*>k can look inconsistent enough to raise doubts about whether there’s any real pattern present at all. But the method I’ve described does still provide a kind of quantitative confirmation for the correlations I mentioned earlier—
- y*>k: 1053 actual, 809 predicted (~130%)
- y*>t: 764 actual, 377 predicted (~203%)
- n*>k: 500 actual, 425 predicted (~118%)
- n*>t; 423 actual, 231 predicted (~183%)
- e*>y: 3238 actual, 2472 predicted (~131%)
- ee*>y: 1258 actual, 918 predicted (~137%)
—as well as evidence for numerous others besides. Here’s a list of further general cases with actual-to-predicted ratios less than 3:5 or greater than 5:3 and actual counts exceeding 100, with all manifestations of each having an actual count or prediction of ten or higher given afterwards together with their individual ratios (predictions are rounded to nearest integer, which will occasionally give the illusion of a tie when values are only very close).
- n*>cKh: 129 actual, 54.75 predicted (~236%): nch>cKh (85:32), nSh>cKh (34:15)
- e*>d: 513 actual, 245.98 predicted (~209%): eo>d (380:105), ech>d (18:11); exception: ey>d (85:101)
- q*>k: 2610 actual, 1275.42 predicted (~205%): qo>k (2591:1273); qe>k (15:1)
- y*>p: 148 actual, 73.15 predicted (~202%): yo>p (108:57), yy>p (21:3)
- k*>ch: 166 actual, 88.67 predicted (~192%): ky>ch (66:43), ke>ch (65:17), kee>ch (23:15), kl>ch (10:6)
- e*>s: 109 actual, 57.06 predicted (~191%): eo>s (66:18), ey>s (35:30)
- cKh*>y: 122 actual, 66.26 predicted (~184%): cKhe>y (72:26), cKhd>y (24:20), cKhh>y (13:10)
- n*>t: 423 actual, 231.14 predicted (~183%): no>t (355:212), ny>t (57:8)
- n*>a: 239 actual, 134.70 predicted (~177%): nd>a (125:42), nch>a (47:33), nSh>a (20:13), ns>a (14:12); exception: no>a (7:14)
- q*>l: 248 actual, 972.28 predicted (~26%): qo>l (247:970)
- y*>y: 263 actual, 857.61 predicted (~31%): yd>y (122:527), yt>y (27:44), yk>y (26:48), ych>y (25:74), ySh>y (14:26), ycTh>y (10:21), yl>y (10:39); exceptions: yr>y (8:16), ys>y (4:15)
- e*>k: 173 actual, 491.19 predicted (~35%): eo>k (70:393), ed>k (8:10); exception: ey>k (91:80)
- ee*>a: 176 actual, 425.26 predicted (~41%): eed>a (106:320), ees>a (26:47), eek>a (11:27), eet>a (5:10); exceptions: eeo>a (12:4), eey>a (12:11)
- d*>k: 191 actual, 421.53 predicted (~45%): dy>k (150:307), do>k (22:85), dl>k (13:15)
- a*>k: 201 actual, 423.07 predicted (~48%): al>k (158:368), ar>k (18:23), ai>k (13:21)
- y*>d: 214 actual, 441.69 predicted (~48%): ych>d (90:138), yl>d (36:58), yo>d (26:159); exception: ySh>d (37:35)
- d*>t: 150 actual, 296.24 predicted (~51%): dy>t (126:244), do>t (23:47)
- e*>a: 581 actual, 1060.66 predicted (~55%): ed>a (392:841), ek>a (63:88), et>a (27:34), es>a (23:40); exceptions: eo>a (32:14), ep>a (12:8), ey>a (11:13)
- l*>y: 336 actual, 565.77 predicted (~59%): ld>y (168:301), lk>y (69:89), lch>y (40:76), lSh>y (26:29), lt>y (4:13), ll>y (3:10)
I’ve marked a specific transition as an “exception” whenever its ratio of predicted to actual occurrences tips in the opposite direction from the ratio for its group as a whole, ignoring the magnitude of the difference, which, as I’ve noted, can very a great deal. Based on that criterion, all the individual transitions listed here with either actual counts or predictions greater than 101 conform to the general pattern, while the values for the most frequent “exceptions” are comparatively close: 85:101 (~84%), 91:80 (~114%), 37:35 (~106%). My impression is that the patterns are consistent whenever there’s unquestionably enough data present to overcome random statistical noise. And it certainly looks more likely that l (for example) is having a consistent delayed influence on the probability of y than that ld, lk, lch, lSh, lt, and ll are affecting that probability as independent bigrams that all happen, by pure coincidence, to nudge things in the same direction.
If we were to find evidence only that glyphs can influence the transitions two positions after them rather than just one, that would be noteworthy enough. But we need not stop there. We can also look for delayed influences of glyphs on transitions even further ahead in lines, using the same methods—investigating, for example, y**>k (n+3) or y***>k (n+4) rather than just y>k (n+1) and y*>k (n+2) as we’ve done so far. And it turns out that we can detect some consistent influences at these greater distances as well.
Here’s a list of generic n+3 patterns with an actual-to-predicted ratio less than 4:5 or greater than 5:4 and an actual occurrence count above 100, with all specific manifestations having ten or more actual occurrences or predictions given afterwards with their individual ratios.
- Sh**>q: 353 actual, 239.99 predicted (~147%): Shey>q (148:110), Sheey>q (63:43), ShcKhy>q (20:14), Shed>q (17:7), Shol>q (16:6), Shor>q (10:2); exception: Shdy>q (33:35)
- Sh**>Sh: 103 actual, 71.35 predicted (~144%): Shor>Sh (15:7), Shol>Sh (14:12), Shedy>Sh (13:5); exception: Shey>Sh (11:14)
- p**>a: 111 actual, 77.65 predicted (~143%): pchd>a (26:20), pol>a (16:6), por>a (14:8), pod>a (10:6); exception: par>a (11:11)
- n**>a: 707 actual, 495.71 predicted (~143%): nok>a (202:139), not>a (178:131), nar>a (30:19), nyk>a (28:21), nor>a (27:18), nyt>a (27:17), nche>a (25:13), nod>a (24:13), nol>a (19:17), nchk>a (18:16), nop>a (17:8), nShe>a (14:8), nchd>a (14:9)
- s**>a: 157 actual, 110.55 predicted (~142%): sar>a (46:28), sor>a (25:18), sod>a (15:6), sal>a (12:5), sol>a (10:8), sot>a (10:8); exception: sok>a (8:10)
- a**>m: 110 actual, 79.35 predicted (~139%): ara>m (58:47), ala>m (16:8), alo>m (14:9)
- n**>k: 418 actual, 309.23 predicted (~135%): nqo>k (156:155), nol>k (105:66), nche>k (36:19), nShe>k (24:14), nal>k (18:6), ncho>k (17:12), nShee>k (17:6), nchee>k (14:6)
- t**>d: 410 actual, 318.63 predicted (~129%): tche>d (131:107), teo>d (60:42), tShe>d (36:29), tal>d (34:29), teeo>d (30:24), tol>d (16:9), tcho>d (16:11), tar>d (10:8); exception: teey>d (8:10)
- r**>r: 180 actual, 141.75 predicted (~127%): rai>r (51:44), raii>r (21:11), rcho>r (13:11), rSho>r (10:7); exception: rda>r (15:16)
- k**>k: 141 actual, 219.14 predicted (~64%): keey>k (20:23), kal>k (17:37), kol>k (14:32), kyl>k (12:12), key>k (5:12), keo>k (4:12), kche>k (3:10); exception: kyo>k (36:26)
- ch**>e: 120 actual, 174.24 predicted (~69%): chek>e (13:14), chych>e (12:19), chok>e (11:15). chot>e (3:11); exception: checKh>e (15:15)
- Sh**>a: 183 actual, 257.53 predicted (~71%): Shed>a (63:86), Shod>a (18:22), Shek>a (17:20), Shok>a (10:12), Sheed>a (7:10), Shor>a (5:18)
- a**>ii: 163 actual, 229.20 predicted (~71%): ara>ii (120:165), ala>ii (22:36)
- Sh**>ch: 106 actual, 146.99 predicted (~72%): Shey>ch (19:26), Shol>ch (8:21), Sheey>ch (7:13), Shor>ch (4:10), Shdy>ch (3:11)
- k**>r: 239 actual, 317.55 predicted (~75%): kai>r (78:149), kea>r (12:15), kaii>r (10:21); exceptions: keey>r (33:26), keo>r (25:24), keeo>r (24:20), kcho>r (12:8), keea>r (12:10)
- n**>d: 386 actual, 511.05 predicted (~76%): nche>d (141:222), nShe>d (105:135), nchee>d (20:22), ncho>d (19:20), nShee>d (17:24), nol>d (14:18); exception: nSho>d (12:9)
- ch**>Sh: 125 actual, 165.16 predicted (~76%): chey>Sh (20:25), chdy>Sh (18:24), chol>Sh (13:28), chor>sh (11:14); exception: chal>Sh (10:7)
- a**>ee: 156 actual, 205.87 predicted (~76%): arch>ee (35:41), arSh>ee (28:35), alk>ee (28:43), alSh>ee (20:32), alch>ee (19:29)
- n**>ch: 184 actual, 241.78 predicted (~76%): nol>ch (47:55), not>ch (24:39), nop>ch (23:30), nok>ch (22:26), nal>ch (7:13), nar>ch (4:10)
- k**>a: 373 actual, 487.52 predicted (~77%): kar>a (88:125), ked>a (66:74), keed>a (45:58), kchd>a (16:31), kal>a (11:27); kor>a (9:18); exceptions: kyd>a (41:40), kyr>a (10:6)
- o**>m: 161 actual, 209.56 predicted (~77%): oka>m (52:59), ota>m (50:57), ora>m (18:30), oda>m (15:22), ola>m (6:14)
- n**>e: 184 actual, 237.63 predicted (~77%): not>e (56:69), nok>e (38:68), nyk>e (7:12), nyt>e (4:11); exceptions: nchcKh>e (18:17), nych>e (10:6)
- l**>t: 102 actual, 130.35 predicted (~78%): lche>t (2:12); exception: lqo>t (60:56)
In several cases, there are so many exceptions that the validity of a given pattern might seem doubtful. But many other patterns are impressively consistent. It would, for example, be hard to deny that the presence of n correlates with an increased probability that the glyph three positions ahead will be a or k rather than ch. Indeed, this point would seem to be statistically indisputable, as far as it goes; the only question is what’s causing the differences in probability.
Moving on to the n+4 category, we find numerous patterns that seem even more consistent than those in the n+3 category. Note that at this point we’ve exceeded the length of a four-glyph word, so that we’ll increasingly be comparing the beginning of one word with the beginning of the next word, the end of one word with the end of the next word, the middle of one word with the middle of the next word, and so forth. Here’s a list of generic n+4 patterns with an actual-to-predicted ratio less than 5:6 or more than 6:5, with over 100 occurrences, and with all manifestations having at least ten actual or predicted occurrences given afterwards with their individual ratios.
- ee***>ee: 175 actual, 115.01 predicted (~152%): eeyok>ee (33:19), eeylk>ee (25:20), eeyot>ee (24:13), eeolk>ee (13:8), eedych>ee (10:9), eeyqo>ee (10:4)
- t***>t: 176 actual, 117.67 predicted (~150%): taro>t (30:19), teeyo>t (23:12), talo>t (17:10), tedy>t (12:8), tolo>t (11:5), tyqo>t (11:6)
- Sh***>q: 541 actual, 381.24 predicted (~142%): Shedy>q (317:237), Sheedy>q (56:47), Sheol>q (37:19), ShecKhy>q (19:12), Shody>q (11:9), ShecThy>q (10:7)
- e***>i: 109 actual, 79.90 predicted (~136%): eoda>i (23:17), eyda>i (15:8), eyka>i (13:9)
- n***>a: 413 actual, 326.83 predicted (~126%): nqok>a (76:57), nolk>a (43:35), nched>a (28:19), nqot>a (24:19), nchek>a (15:11), nShed>a (12:9), nalk>a (11:9), nchot>a (10:7)
- Sh***>Sh: 122 actual, 96.71 predicted (~126%): Shedy>Sh (37:32)
- o***>ee: 193 actual, 155.21 predicted (~124%): olok>ee (15:15), orok>ee (13:8), olot>ee (12:9), odych>ee (10:6)
- s***>e: 122 actual, 98.83 predicted (~123%): solch>e (22:18), solSh>e (19:14), salch>e (14:8), solk>e (10:6)
- d***>d: 704 actual, 572.07 predicted (~123%): dyche>d (135:114), dyShe>d (76:56), daiin>d (54:32), dyqo>d (33:31), dyte>d (33:28), dyke>d (19:16), darch>d (17:12), dain>d (15:10), dykee>d (14:9), dychee>d (13:12), dkch>d (12:6); exception: dycho>d (14:15)
- p***>a: 112 actual, 91.71 predicted (~122%): pched>a (31:26)
- ee***>d: 113 actual, 158.39 predicted (~71%): eeyche>d (18:23), eedych>d (8:10), eeyShe>d (7:10)
- y***>q: 194 actual, 252.68 predicted (~77%): yShey>q (28:29), ychey>q (17:23), ySheey>q (12:14), yteey>q (9:10), ykeey>q (8:12), ychdy>q (8:11); ydal>q (5:10); exception: ycheey>q (14:12)
- q***>o: 242 actual, 314.96 predicted (~77%): qoke>o (60:77), qokee>o (47:57), qote>o (26:31), qoky>o (17:18), qotee>o (14:14), qotch>o (10:12), qokch>o (8:17), qoty>o (6:13)
- e***>d: 242 actual, 314.44 predicted (~77%): edych>d (20:22), eyche>d (11:21); edySh>d (7:10), edal>d (5:10), eody>d (3:11); exception: eolch>d (10:7)
- Sh***>d: 117 actual, 150.68 predicted (~78%): Shedy>d (25:42)
- l***>k: 144 actual, 184.48 predicted (~78%): lchey>k (8:11), lchol>k (8:10)
- ch***>e: 257 actual, 328.05 predicted (~78%): cholch>e (18:30), chdych>e (15:29), cheych>e (14:17), cheeych>e (8:10), cholk>e (4:10)
- ch***>Sh: 167 actual, 210.83 predicted (~79%): chedy>Sh (48:59), cheol>Sh (16:16), cheor>Sh (10:10)
There’s a good deal of overlap between the n+3 and n+4 patterns, which can be seen to some extent in the examples I’ve given (compare Sh**>q and Sh***>q, n**>a and n***>a, Sh**>Sh and Sh***>Sh., p**>a and p***>a, ch**>Sh and ch***>Sh), but which I can see would become even more apparent if we were to compare the whole lists, without applying significance thresholds for quantities or ratios. On the other hand, the fact that the n+4 patterns have so many fewer exceptions than the n+3 patterns hints at some qualitative difference between them as well.
At greater distances such as n+3 and n+4, something we increasingly see among the top entries in our lists is glyph repetitions, such as r**>r or ee***>ee. These patterns indicate that a glyph is more likely than expected to recur after the specified interval, and they become more prevalent yet at n+5 and n+6. Let’s take a closer comparative look at patterns of this special type, setting aside our usual significance thresholds. I’ve highlighted all cases in red where a glyph repetition is not more probable than we’d expect based on lower-level Markov modeling.
- a*>a: 74 actual, 788.71 predicted (~94%); a**>a: 732 actual, 676.91 predicted (~108%); a***>a: 813 actual, 799.07 predicted (~102%); a****>a: 1159 actual, 1144.59 predicted (~101%); a*****>a: 784 actual, 764.51 predicted (~103%)
- ch*>ch: 96 actual, 143.94 predicted (~67%); ch**>ch: 351 actual, 359.89 predicted (~98%); ch***>ch: 483 actual, 462.43 predicted (~104%); ch****>ch: 435 actual, 393.23 predicted (~111%); ch*****>ch: 428 actual, 367.87 predicted (~116%)
- cKh*>cKh: 0 actual, 2.67 predicted (0%); cKh**>cKh: 4 actual, 3.80 predicted (~105%); cKh***>cKh: 7 actual, 3.59 predicted (~195%), cKh****>cKh: 7 actual, 2.91 predicted (~241%); cKh*****>cKh: 2 actual, 1.64 predicted (~122%)
- d*>d: 418 actual, 483.03 predicted (~87%); d**>d: 331 actual, 298.94 predicted (~111%); d***>d: 704 actual, 572 predicted (123%); d****>d: 859 actual, 775.48 predicted (~111%); d*****>d: 1226 actual, 1088.41 predicted (~113%)
- e*>e: 151 actual, 198.26 predicted (~76%); e**>e: 50 actual, 46.83 predicted (~107%); e***>e: 602 actual, 587.56 predicted (~102%); e****>e: 639 actual, 606.99 predicted (~105%); e*****>e: 623 actual, 573.66 predicted (~109%)
- ee*>ee: 15 actual, 35.47 predicted (~42%); ee**>ee: 50 actual, 46.83 predicted (~107%); ee***>ee: 175 actual, 115.01 predicted (~152%); ee****>ee: 224 actual, 160.43 predicted (~140%); ee*****>ee: 207 actual, 156.69 predicted (132%)
- i*>i: 1 actual, 0.33 predicted (~299%); i**>i: 732 actual, 676.91 predicted (~108%); i***>i: 14 actual, 16.62 predicted (~84%); i****>i: 69 actual, 62.57 predicted (~110%), i*****>i: 53 actual, 38.30 predicted (~138%)
- ii*>ii: 0 actual, 0.10 predicted (0%); ii**>ii: 15 actual, 16.08 predicted (~93%); ii***>ii: 28 actual, 25.63 predicted (~109%); ii****>ii: 128 actual, 119.71 predicted (~107%); ii*****>ii: 79 actual, 68.07 predicted (~116%)
- k*>k: 21 actual, 214.32 predicted (~10%); k**>k: 141 actual, 219.14 predicted (~64%); k***>k: 417 actual, 388.54 predicted (~107%); k****>k: 757 actual, 664.92 predicted (~114%); k*****>k: 742 actual, 682.10 predicted (~109%)
- l*>l: 427 actual, 359.53 predicted (~119%); l**>l: 336 actual, 362.66 predicted (~93%); l***>l: 416 actual, 377.74 predicted (~110%); l****>l: 441 actual, 378.87 predicted (~116%); l*****>l: 408 actual, 361.46 predicted (~113%)
- m*>m: 4 actual, 0.63 predicted (~631%); m**>m: 4 actual, 0.64 predicted (~624%); m***>m: 9 actual, 1.51 predicted (~596%); m****>m: 7 actual, 1.07 predicted (~654%); m*****>m: 0 actual, 0.81 predicted (0%)
- n*>n: 3 actual, 1.25 predicted (~239%); n**>n: 26 actual, 33.36 predicted (~78%); n***>n: 67 actual, 69.42 predicted (~97%); n****>n: 298 actual, 299.23 predicted (~100%); n*****>n: 187 actual, 186.25 predicted (~100%)
- o*>o: 1301 actual, 1424.99 predicted (~91%); o**>o: 1226 actual, 1283.98 predicted (~95%); o***>o: 1602 actual, 1532.73 predicted (~105%); o****>o: 2202 actual, 2169.40 predicted (~102%); o*****>o: 2255 actual, 2186.48 predicted (~103%)
- p*>p: 0 actual, 7.21 predicted (0%); p**>p: 6 actual, 7.12 predicted (~84%); p***>p: 17 actual, 8.16 predicted (~208%), p****>p, 35 actual, 13.03 predicted (~269%); p*****>p: 45 actual, 15.26 predicted (~295%)
- q*>q: 8 actual, 18.54 predicted (~43%); q**>q: 6 actual, 21.51 predicted (~28%); q***>q: 39 actual, 35.74 predicted (~109%); q****>q: 244 actual, 224.65 predicted (~109%); q*****>q: 451 actual, 437.26 predicted (~103%)
- r*>r: 404 actual, 402.87 predicted (~100%); r**>r: 180 actual, 141.75 predicted (~127%); r***>r: 240 actual, 215.39 predicted (~111%); r****>r: 175 actual, 165.56 predicted (~106%); r*****>r: 180 actual, 161.23 predicted (~112%)
- s*>s: 15 actual, 10.47 predicted (~143%); s**>s: 18 actual, 12.26 predicted (~146%); s***>s: 23 actual, 11.77 predicted (~195%); s****>s: 17 actual, 9.68 predicted (~176%); s*****>s: 20 actual, 16.29 predicted (~123%)
- Sh*>Sh: 12 actual, 19.72 predicted (~61%); Sh**>Sh: 103 actual, 71.35 predicted (~144%); Sh***>Sh: 122 actual, 96.71 predicted (~126%); Sh****>Sh: 102 actual, 66.92 predicted (~152%); Sh*****>Sh: 102 actual, 67.05 predicted (~152%)
- t*>t: 18 actual, 79.89 predicted (~23%); t**>t: 71 actual, 63.52 predicted (~112%); t***>t: 176 actual, 117.67 predicted (~150%); t****>t: 292 actual, 198.19 predicted (~147%); t*****>t: 211 actual, 141.15 predicted (149%)
- y*>y: 263 actual, 857.61 predicted (~31%); y**>y: 734 actual, 907.02 predicted (~81%); y***>y: 1594 actual, 1593.97 predicted (~100%); y****>y: 1735 actual, 1675.93 predicted (~104%); y*****>y: 1546 actual, 1496.38 predicted (~103%)
In nearly every case, glyph repetitions at distances beyond n+3 are more common than expected. In other words, the probability of a transition to a glyph almost always increases if that glyph has appeared in the recent (but not immediate) past.
We might conjecture that specific glyphs are statistically more likely to repeat because they already happen to be concentrated in certain parts of lines and paragraphs. That is, an Sh might be more likely than usual to occur after another Sh only because tokens of Sh have a higher overall concentration earlier in lines than elsewhere, and p might be more likely than usual to occur after another p just because tokens of p have a higher overall concentration in the first lines of paragraphs than elsewhere. However, most glyphs show a greater likelihood of repeating only after a certain interval and are actually less likely to repeat beforehand than lower-order Markov analyses would predict. Moreover, I’ve found that if I work out counts, probabilities, and predictions separately for each segment of the line or paragraph, the same basic patterns seem to persist. Thus, the increased probability of repetitions doesn’t appear to result merely from positional differences in concentration.
Since the generic glyph-by-glyph probabilities we’re using as a point of reference are calculated from all occurrences, including the ones that would involve glyphs recurring at n+2 and n+3, recurrences at n+4 and after could conceivably appear more probable than average only by contrast with the less-probable occurrences at n+2 and n+3. This might account for cases in which a glyph is so common that transitions at n+2 and n+3 from it form a significant proportion of the whole. But it surely couldn’t apply to some of the most notable cases, such as cKh, Sh, and s, so I don’t think it can be the only or primary explanation for the patterns were seeing.
I’ll call this the persistence principle: after a glyph appears once, the probability of another transition to that same glyph increases—as noted, often after a short interval before which it tends instead to decrease. Here’s the data for several selected glyphs displayed graphically:
Let’s consider how this principle plays out for one category of glyphs in which the variants seem at least somewhat structurally interchangeable.
Gallows glyphs are much less likely than a first-order Markov analysis would predict to repeat identically at n+2; for example, even though t>o and o>t might individually both be fairly probable, the combination of the two as t>o>t is far less so. At n+3, t is more likely to repeat than expected, while k and p are still a little less likely to repeat than expected; and then, at n+4, n+5, and n+6, t and p are both much more likely to repeat than expected, while k is only slightly more likely. But here it’s important to observe that in terms of absolute numbers, repetitions of k far exceed repetitions of t and p. Remember that what we’re tracking here is differences in probability relative to what lower-order Markov analysis would predict, and that k is part of the qokeedy loop—which is to say, it’s already bound up in a default tendency to repeat, even in a first-order Markov analysis. Thus, even if k repeats more often than t does in absolute terms, we’d expect it to do that regardless of whether the first k has any effect on the probability of the second one or not.
This circumstance may be easier to grasp if we take a look at specific sequences in which k or t repeats at n+5 or n+6.
- kedyqo>k: 109 actual, 94.09 predicted (~116%)
- keedyqo>k: 165 actual, 156.84 predicted (~105%)
- keyqo>k: 32 actual, 27.47 predicted (~116%)
- keeyqo>k: 109 actual, 92.48 predicted (~118%)
- kedyo>k: 62 actual, 42.03 predicted (~148%)
- keedyo>k: 41 actual, 37.52 predicted (~109%)
- tedyqo>t: 34 actual, 16.75 predicted (~203%)
- teedyqo>t: 30 actual, 18.77 predicted (~160%)
- teyqo>t: 3 actual, 2.87 predicted (~105%)
- teeyqo>t: 13 actual, 9.14 predicted (~142%)
- tedyo>t: 29 actual, 25.29 predicted (~115%)
- teedyo>t: 17 actual, 14.56 predicted (~117%)
There are (to choose just one pair of cases) more occurrences of kedyqo>k than there are of tedyqo>t, but tedyqo>t exceeds expectations for *edyqo>t by a greater ratio than kedyqo>k exceeds expectations for *edyqo>k.
Let’s now look at the likelihood of a given gallows glyph being followed by a different gallows glyph at these same intervals.
- k*>p: 4 actual, 28.25 predicted (~14%); k**>p: 13 actual, 25.56 predicted (~51%); k***>p: 36 actual, 47.71 predicted (~75%); k****>p: 44 actual, 31.13 predicted (~141%); k*****>p: 38 actual, 48.46 predicted (78%)
- k*>t: 11 actual, 104.81 predicted (~11%); k**>t: 73 actual, 106.64 predicted (~68%); k***>t: 181 actual, 207.69 predicted (~87%); k****>t: 63 actual, 47.18 predicted (~134%); k*****>t: 224 actual, 253.46 predicted (~88%)
- p*>k: 9 actual, 61.94 predicted (~15%); p**>k: 32 actual, 56.97 predicted (~56%); p***>k: 33 actual, 40.54 predicted (~81%); p****>k: 18 actual, 21.58 predicted (~83%); p*****>k: 51 actual, 67.01 predicted (~76%)
- p*>t: 2 actual, 33.56 predicted (~6%); p**>t: 12 actual, 20.83 predicted (~57%); p***>t: 21 actual, 19.78 predicted (~106%); p****>t: 26 actual, 15.93 predicted (~163%); p*****>t: 35 actual, 40.74 predicted (~86%)
- t*>k: 20 actual, 154.84 predicted (~13%); t**>k: 76 actual, 144.34 predicted (~53%); t***>k: 153 actual, 189.52 predicted (~81%); t****>k: 53 actual, 37.82 predicted (~140%); t*****>k: 280 actual, 309.49 predicted (90%)
- t*>p: 3 actual, 19.56 predicted (~15%); t**>p: 17 actual, 16.67 predicted (~102%); t***>p: 27 actual, 27.91 predicted (~97%); t****>p: 30 actual, 22.57 predicted (~132%); t*****>p: 38 actual, 32.70 predicted (116%)
We find that there’s a much lower probability of a gallows glyph in general—regardless of type—repeating at n+2 than a first-order Markov analysis would predict. This is presumably why my random simulation based on first-order matrices generated so many more words containing multiple gallows glyphs than my random simulation based on second-order matrices did. At greater distances, however, one given gallows glyph sometimes proves to be more likely than expected to be followed by a different given gallows glyph, and not only by the same one again. When the first glyph is p or t, the increase in probability that the same glyph will repeat is invariably greater for n+3, n+4, n+5, and n+6 than the increase in probability that some other gallows glyph will follow; but this isn’t always true if the first glyph is k. Meanwhile, the increased probability of transition to a different gallows glyph—irrespective of the probability of transition to the same gallows glyph—appears to peak strongly at n+5 and then to decline at n+6.
If we look at an equivalent set of specific examples to the ones we considered above, but now displaying a change from k to t or vice versa, we find that most of them turn out to be less probable than expected.
- kedyqo>t: 19 actual, 29.51 predicted (~64%)
- keedyqo>t: 45 actual, 53.19 predicted (~85%)
- keyqo>t: 4 actual, 5.73 predicted (~70%)
- keeyqo>t: 22 actual, 27.43 predicted (~80%)
- kedyo>t: 35 actual, 42.03 predicted (~83%)
- keedyo>t: 40 actual, 39.76 predicted (~101%)
- tedyqo>k: 42 actual, 53.40 predicted (~79%)
- teedyqo>k: 47 actual, 55.35 predicted (~85%)
- teyqo>k: 15 actual, 13.74 predicted (~109%)
- teeyqo>k: 28 actual, 30.83 predicted (~91%)
- tedyo>k: 18 actual, 25.29 predicted (~71%)
- teedyo>k: 13 actual, 13.74 predicted (~95%)
Singling out one pair of cases by way of illustration, there may be more occurrences of tedyqo>k (42) than there are of tedyqo>t (34), but *edyqo>k is also more common than *edyqo>t in general, such that tedyqo>k occurs only ~79% as often as expected, while tedyqo>t occurs ~203% as often. Out of all our “mixed” examples, only keedyo>t and teyqo>k occur more rather than less often than expected, and only teyqo>k (~109%) exceeds expectations by a wider ratio than the corresponding teyqo>t (~105%)—a razor-thin exception that just one more occurrence of teyqo>t, or one fewer of teyqo>k, would have reversed.
Approaching things from yet another direction, we can calculate entire transitional probability matrices for t**o, k**o, t***o, k***o, t****o, and k****o and then compare them against the generic transitional probability matrix for o, option by option.
- o>k = 30.31%
- t**o>k = 17.75%; t***o>k = 24.93%; t****o>k = 33.04%
- k**o>k = 32.68%; k***o>k = 39.18%; k****o>k = 46.81%
- o>l = 23.25%
- t**>ol = 23.26%; t***o>l = 17.01%; t****o>l = 13.84%
- k**o>l = 22.82%; k***o>l = 21.40%; k****o>l = 17.70%
- o>t = 16.83%
- t**o>t = 29.02%; t***o>t = 34.03%; t****o>t = 28.03%
- k**o>t = 19.30%; k***o>t = 21.86%; k****o>t = 15.27%
- o>r = 8.90%
- t**o>r = 9.59%; t***o>r = 5.97%; t****o>r = 7.96%
- k**o>r = 9.72%; k***o>r = 5.70%; k****o>r = 5.84%
- o>d = 8.03%
- t**o>d = 8.39%; t***o>d = 5.37%; t****o>d = 7.27%
- k**o>d = 6.20%; k***o>d = 3.54%; k****o>d = 5.84%
A return to the same gallows glyph consistently shows a boost in probability at n+4, n+5, and n+6 (highlighted in blue). A transition to a different gallows glyph sometimes also shows a boost in probability (highlighted in green), but never by nearly as much, and not consistently, except that the probabilities of transition to either glyph type seem to rise and fall together. Meanwhile, transitions to non-gallows glyphs regularly show a decrease in probability at n+5 and n+6.
To summarize:
- Once a t occurs, there’s a heightened probability of the same choice of t persisting when another opportunity arises for it to be made four, five, or six places later.
- Once a k occurs, there’s a heightened probability of the same choice of k persisting when another opportunity arises for it to be made four, five, or six places later.
- Once any gallows glyph occurs, there’s a more weakly heightened probability of a different gallows glyph being chosen when another opportunity arises for it to be made four, five, or six places later.
It’s worth pointing out that the sequences we’ve just been considering routinely span word breaks (e.g., qotedy.okedy), such that in a word-centered analysis of Voynichese, we might instead have been examining the likelihood of a word containing one gallows glyph being followed by a word containing the same gallows glyph or a different one.
We can generalize to say that, after a token of a glyph occurs:
- Transition back to the same glyph is typically inhibited for a couple positions (but not wholly forbidden).
- After that interval, transition back to the same glyph typically becomes more probable than usual.
- Transition to certain “similar” glyphs may be constrained in the same way, but more weakly.
Each piece of this model has its exceptions. For example, l seems not to be inhibited from immediate repetition, while n seems not to favor repetition at all, at least within six places. But the model typically pertains; the majority of glyphs behaves as I’ve described.
I argued above that the default overall tendency of the script is to fall into a repeating loop and to fall back into it again after an escape. But now it appears that there’s also a tendency for specific deviations from the loop—such as the choice of t rather than k—to persist, as well as for the choice of a first option—such as k in the context of the qokeedy loop—to boost its future probability even beyond its usual high level. Past glyph choices seem to influence future glyph choices; the process of text creation seems to have a memory.
Remember that we’re not tracking the absolute probabilities of a glyph recurring after a certain interval, but the differences between those probabilities and the ones which more local conditions would ordinarily predict: ko>k as opposed to o>k, kol>k as opposed to ol>k, and so on. So the differences in probability I’ve reported between k*>k, k**>k, k***>k, k****>k, and k*****>k don’t simply arise out of the cumulative glyph-by-glyph transitional probabilities across those distances. They’re superimposed on those other probabilities as a modification of them.
At the distances we’ve been considering, glyph recurrences are likely to affect pairs of consecutive words. The persistence principle would thus predict that similar words should have a greater likelihood of appearing next to each other within lines than dissimilar ones, with the average degree of similarity decreasing with distance. This prediction is consistent with Timm’s observations about co-occurrence patterns within lines.
If we return to the set of the longest identically repeating glyph sequences, at least a couple of them appear to display persistent patterns of deviation from the qokeedy loop if we admit ch and Sh as similar glyphs, with a relationship to each other analogous to that of the various gallows glyphs.
- olchedyqokainolSheyqokain
- Shedyqokalchedyqokaiin
Now, I’ll admit that these two examples might complicate the line of argument I’ve been laying out as much as they support it. For one thing, their periods of repetition are significantly longer than n+6. In the first example, using my usual criteria for what counts as a single glyph, it’s n+12 (l>ch>e>d>y>q>o>k>a>i>n>o>l). In the second example, it’s n+9 (Sh>e>d>y>q>o>k>a>l>ch). Moreover, in the first example, the transitions from o end up alternating: first o>l, then o>k, then o>l again, then o>k again. It’s true that these transitions are the most probable ones for their contexts: compare edyqo>k (63.57%) with edyqo>l (7.10%) and kaino>l (35.96%) with kaino>k (28.09%). But it would seem disingenuous to claim that there’s anything persistent about the transitions from o as such. We might still say that the transitions l>ch/Sh and k>a are persistent, in that they occur twice in a row, even though l>k and k>e+ is ordinarily a little more probable, and that the rest of the repeating pattern (insofar as it repeats) follows from that, including the alternation in transitions from o. In the second example, the transition to ch/Sh and the choice of k>a over k>e+ again seem to be the persistent elements, which would make for an interesting coincidence. Maybe I shouldn’t make too much of these sequences, but the fact that they occur not just once but twice, when identical repetitions of this length are so rare, suggests to me that there must be something unusually probable about their structures. Perhaps there’s a larger default structure something along the lines of qokaiinolchedy—a structure which the sequence qokeedy short-circuits (so to speak) in the same way that chedy short-circuits qokeedy.
This seemingly variable period of repetition poses a frustrating practical obstacle to analyzing Voynichese in cyclical terms. Although I’ve been examining distances between glyphs such as n+4, n+5, n+6, and so on, I doubt these categories are really meaningful. Most researchers sidestep the need to identify cyclical units by studying words (or “vords”) rather than continuous sequences, but I don’t have that luxury because I don’t want to assume that spaces consistently mark definitive boundaries, or that or.aiin and oraiin (for example) fall into wholly different analytical categories, with the one being a pair of words and the other being a single word, and never the twain shall meet. But it’s challenging to gauge such phenomena as persistence without a consistent cycle length across which glyph choices can persist (or not), at least in any large-scale quantitative way. So I’m tempted to fall back on words, to a limited extent, despite my general misgivings about their reliability as objects of study.
One case in which I’m comfortable analyzing words is when a significant portion of two successive words is identical, as with qokeedy.chedy. In these situations, I believe it’s reasonably safe to interpret the two words as corresponding to two cycles—or, if you will, two passes through a sequence of transitions that returns each time to an equivalent point. (I’ll even agree that a majority of words probably do represent discrete cycles; I just don’t believe they always do.)
With that in mind, let’s take a look at some generic cases of partial repetition in which the repeated element is indicated by an asterisk (*). In my counts, I’ll include cases in which the second word continues beyond the repetition (e.g., cheod.qokeody would count as a manifestation of ch*.ok*), and I’ll also treat e+ sequences differently here than usual (in that an example of ch*.qoke* would be chedy.qokeedy; ordinarily, in the terms laid out above, I’d be parsing these words as ch-e-dy and q-o-k-ee-d-y).
- ch*.qok* = 28, Sh*.qok* = 34, ch*.qoke* = 18, Sh*.qoke* = 18, che*.qok* = 5, She*.qok* = 7
- qok*.ch* = 19, qok*.Sh* = 14, qoke*.ch* = 16, qoke*.Sh* = 7; qok*.che* = 4, qok*.She* = 4
In the qokeedy loop, an alternative transition to ch or Sh tends by default to lead from y back to ee, such that we could say that ch and Sh are filling an analogous role in the loop to that of qok. But judging from the above examples, it looks as though a choice of ch or Sh is distinctly more likely to be followed by a choice of qok than the other way around—about 1.7 times more likely on average. For want of a better word, I’ll refer to a change from one transitional choice to a different transitional choice between two loop iterations as flipping, as in: it’s about 1.7 times more likely for ch or Sh to flip to qok than for qok to flip to ch or Sh (still judging only from the few cited examples). Moreover, the disparity is markedly greater for Sh than it is for ch. It’s about 1.3 times more likely for ch to flip to qok than for qok to flip to ch, but it’s about 2.4 more likely for Sh to flip to qok than for qok to flip to Sh.
Given this asymmetrical relationship between Sh and qok, we would expect, all other things being equal, that the frequency of Sh would decrease relative to the frequency of qok over the course of a line, with Sh losing ground through attrition and qok gaining it. That’s not quite what we see. However, Sh does decline steadily in frequency over the course of a line, while q rises to a mid-line peak before declining in frequency towards the end (which is probably also true of qok as the most probable sequence starting at q). This is at least somewhat like what the foregoing would predict.
It seems to me that the cumulative result of multiple asymmetric probabilities of flipping could potentially give us the differences in glyph distributions and transitional probabilities within lines considered above in section two. In fact, I’ll go further: the sum total of all cases must ultimately produce those differences in one way or another. But I’ll confess that, at the moment, I’m unsure how best to go about investigating the specifics further on a large scale. To study the probability of particular flips, we’d need to be consistently sure about identifying which elements are equivalent, as is presumptively the case above with Sh, ch, and qok, and I don’t think we are—or at least that I am.
Still, we can probably also bring the persistency principle—and the complementary concept of flipping—to bear on conspicuously repetitious sequences such as the line taiin.ytaiin.ytaiin.ytaiin.ar.ar.ytar.am (f86v3, my own reading from the facsimile), which I’ve previously shown formatted as a “cycle chart” (here, at section five):

If we were to analyze this sequence in terms of transitional probabilities, we’d have to say that the transitions are remarkably persistent over the first few cycles, producing three identical words, until we finally hit an occurrence of n>a instead of n>y. Zandbergen actually transcribes this particular a as o, and statistics based on the Zandbergen transcription (for Currier B) show taiin>o with a probability of 42.37%, taiin>y at 8.05%, and taiin>a at 5.08%. But it looks to me as though the glyph in question is closed with a minim, at the same length and angle as some of the minims in the preceding word, which would place it in the a category for me. Some of the other reported cases of taiin>o might likewise be better identified as taiin>a in my judgment, so perhaps the latter transition is more probable than my statistics would suggest.
 In any case, the transition a>r now seems to supersede or overwrite the formerly persistent a>ii>n. (I count thirteen cases of *iin.*r and seventeen of *r.*iin, so flipping from *iin to *r appears to be slightly less common than the reverse, but still not uncommon.) This new choice loops as a>r>a>r; but then we encounter a single occurrence of r>y, which, like l>y, is much more probable later in a line than earlier. This is followed by a repetition of the formerly persistent y>t>a transitions, which still seem to be “in effect,” as it were. But a>r>a now seems to have become persistent too; instead of returning to y>t>a>ii>n, we get y>t>a>r>a, and then r flips to m to complete the line, consistent with the heightened probability of a flip to m in that position. There’s some further uncertainty here as to the glyphs themselves; Zandbergen shows yta[s:r], although the base of the final glyph looks unambiguously like a minim to me, which would place it squarely in the r category. If the persistence principle really pertains, it might conceivably have helped someone who understood the writing system to disambiguate graphemes while reading that can’t otherwise be told clearly apart. There are, I’m sure, many other ways in which the patterning of this particular line could be analyzed; but I think a combination of transitional probabilities, persistence, and flipping can accommodate its quirks rather elegantly.
In any case, the transition a>r now seems to supersede or overwrite the formerly persistent a>ii>n. (I count thirteen cases of *iin.*r and seventeen of *r.*iin, so flipping from *iin to *r appears to be slightly less common than the reverse, but still not uncommon.) This new choice loops as a>r>a>r; but then we encounter a single occurrence of r>y, which, like l>y, is much more probable later in a line than earlier. This is followed by a repetition of the formerly persistent y>t>a transitions, which still seem to be “in effect,” as it were. But a>r>a now seems to have become persistent too; instead of returning to y>t>a>ii>n, we get y>t>a>r>a, and then r flips to m to complete the line, consistent with the heightened probability of a flip to m in that position. There’s some further uncertainty here as to the glyphs themselves; Zandbergen shows yta[s:r], although the base of the final glyph looks unambiguously like a minim to me, which would place it squarely in the r category. If the persistence principle really pertains, it might conceivably have helped someone who understood the writing system to disambiguate graphemes while reading that can’t otherwise be told clearly apart. There are, I’m sure, many other ways in which the patterning of this particular line could be analyzed; but I think a combination of transitional probabilities, persistence, and flipping can accommodate its quirks rather elegantly.
The persistence principle might also account in part for the distinctive distribution of p and f. We may not know why p is so common as the first glyph of a paragraph. But given that it is, the persistence principle would predict it should also have a greater-than-usual probability further along in the same (first) lines, and that similar glyphs should also experience a boost in probability there, though more weakly. Thus, the widely recognized preference of p and the morphologically similar f for the first lines of paragraphs might be an expected consequence of the commonness of p as the first glyph of a paragraph, with no need to seek any further explanation. Likewise, repetitions of the rare x (xor.xoiin, xar.odas.xaloeees) look very much like cases of persistence within a particular cyclical slot. If there were no tendency in favor of persistence, the odds against two tokens of x appearing in such close proximity would be astronomical.
§ 4
The Limits of LAAFU
I mentioned earlier that I wasn’t sure there’s any “pure” point of reference for a transition such as *o>k that’s truly neutral with regard to preceding glyphs. If there is, however, the best candidate would probably be the first transition of a line. If all *o>k transitions appearing later in lines are contaminated by the influence of other more distantly preceding glyphs, we might suppose that line-initial ok could uniquely reveal the “true” probability for that transition entirely on its own. In line-initial position, o has the following transitional counts and probabilities (out of 296 total lines; remember also that we’re still limiting our analysis to Currier B):
- o>l (79) = 26.69%
- o>k (73) = 24.66%
- o>t (48) = 16.22%
- o>r (23) = 7.77%
- o>a (16) = 5.41%
- o>d (12) = 4.05%
But even these line-initial transitions still have contexts that could affect their probability matrices. If we calculate probabilities for specific paragraph sectors, the results turn out to be somewhat different (gallows more likely in the first line, k more likely in the middle and last thirds, l more likely in the first third or the last line, d more likely further downward in a paragraph).
- First line: o>t = 35.29%, o>k = 29.41%
- First third: o>l = 26.76%, o>k = 20.88%, o>t = 13.19%, o>a = 7.69%, o>r = 5.49%
- Middle third: o>k = 26.76%, o>l = 19.72%, o>t = 16.90%, o>r = 14.08%, o>a = 7.04%
- Last third: o>k = 27.08%, o>l = 22.92%, o>t = 14.58%, o>d and o>a = 6.25%
- Last line: o>l = 31.88%, o>k = 24.64%, o>t = 15.94%, o>d and o>r = 7.25%
Another indication that successive lines aren’t wholly independent from one another is Timm’s observation that “similar” words are more likely to appear in the same position within a line the closer the lines are to each other, and that “similar” sequences with rare characteristics are often found appearing on separate lines near each other within paragraphs more generally (to cite just one example, witness oxar four lines after ox,o,r on f111r).
Meanwhile, the relative frequencies of the first glyphs of lines also vary quite a lot by paragraph position, not just with gallows in the first lines of paragraphs (as is easy to see), but with lower lines and other glyph types as well. This too suggests that even if the line behaves as a functional unit in some respects, lines aren’t composed in ways that are wholly independent of their contexts either; or, in other words, that they don’t start over wholly from scratch each time with a clean slate. Nobody was reaching into a hat and pulling out lines at random.
The above graphs doubtless show effects of random statistical noise, but some consistent patterns are worth pointing out across the two Currier “languages”:
- The phenomenon by which gallows glyphs overwhelmingly dominate the starts of the first lines of paragraphs, especially p and t, is well known, and it’s so strong that I’ve had to let p ascend off the chart in order to present the rest of the statistics at intelligible scale.
- Elsewhere in paragraphs, t is usually the most common line-initial gallows glyph, except for the first glyph of the last line of a paragraph in Currier B, where k peaks as line-initial.
- During the first third of the paragraph, the most common line-initial glyph is d.
- In the last line of a paragraph, the most common line-initial glyph is y.
- Line-initial q peaks in the middle of paragraphs.
For what it’s worth, the relative frequencies of the last glyphs of lines are rather more consistent for different paragraph sectors, though not entirely consistent.
In Currier A, line-final n is more common than line-final m, while in Currier B, it’s usually the other way around, except for the last line in a paragraph, where n overtakes m. Otherwise, line-final s, g, and d are a bit more common in Currier A, and line-final l is a bit more common in Currier B. Across both “languages,” y dips noticeably in mid-paragraph and n becomes more common further downward. In general, though, the beginnings of lines are more positionally variable and diverse than the ends of lines are.
The transition from the last glyph of one line to the first glyph of the next line displays distinct patterns as well. As I observed earlier here, at section four, lines ending m are followed by lines ending q only 58.3% as often as we’d expect from random shuffling—with this statistic pertaining to both “languages” assessed together. If we limit our scope to Currier B and calculate transitional probabilities rather than absolute frequencies, we find that the top six transitions across line breaks order themselves as follows, with the transitions to q highlighted in blue:
- y (864): y>d (19.21%), y>y (16.44%), y>q (15.97%), y>s (14.47%), y>o (11.69%), y>t (7.18%)
- m (433): m>y (21.02%), m>d (20.55%), m>s (16.17%), m>o (12.47%), m>t (7.85%), m>q (7.62%)
- n (222): n>y (18.47%), n>s (16.22%), n>d (15.32%), n>o (13.96%), n>q (13.51%), n>t (7.21%)
- l (273): l>d (19.41%), l>q (16.85%), l>y (16.48%), l>s (16.12%), l>o (10.62%), l>t (5.49%)
- r (174): r>d and r>y (18.97%), r>o (18.39%), r>q (16.09%), r>s (9.20%), r>ch (5.17%)
- d (52): d>q (21.15%), d>d (19.23%), d>o (17.31%), d>y (9.62%), d>s (9.62%), d>l (7.69%)
- s (49): s>q (24.49%), s>s (20.41%), s>o (16.33%), s>y (12.24%), s>d (10.20%), s>Sh (6.12%)
- g (41): g>d and g>q (17.07%), g>o and g>y (14.63%), g>t (12.20%), g>s (9.76%)
Here, too, we can see that the probability of a line-break transition to q is conspicuously lower after m than it is after any other glyph, with n coming closest. Meanwhile, it’s conspicuously higher after d and s (both of which are, however, comparatively uncommon line-end glyphs in the first place). A line ending in s is over three times more likely to be followed by a line beginning with q than a line ending in m is.
These are plainly not the same transitional probabilities we find within lines, where y>d has a probability of only 7.32% and y>y has a probability of only 2.16%. On the other hand, those comparatively rare line-internal transitions do seem to behave similarly to the more common line-break transitions when they do occur. Within lines, yy>k has a probability of 44.64%, and yy>t has a probability of 35.62%—far in excess of the generic probabilities of y>k (6.41%) and y>t (5.16%). With line-initial y in general, y>k has a probability of 20.47% and y>t has a probability of 18.64%; and if we factor in the glyph preceding the line break as well, y/y>k has a probability of 21.83% and y/y>t has a probability of 17.61%. Thus, y/y across a line break, and y in line-initial position more generally, both seem to share a heightened preference for transitions to k and t in common with line-internal yy. Meanwhile, as part of the qokeedy loop, q commonly follows y, but of the many lines beginning y, there isn’t a single one beginning yq with or without a space. Line breaks are special places—no doubt about it.
But whatever factors might be causing line-break transitions to show statistical properties different from line-internal ones, and all the other kinds of subtle variation by line position we’ve been considering, they’re apparently not strong or inflexible enough to render it impossible for formally identical strings to occur in substantially different positions. Consider the positioning of the longest exactly-repeating glyph sequences. Sometimes these share identical positions within or across lines:
- okaiinshedyqokeedyqotedy =
sokcheey.sain.sheeol.qoteedy.qokaiin.shedy.qokeedy.qotedy/ and solchedy.qokain.okaiin.shedy.qokeedy.qotedy/ (both f77r) - daiinchotaiinsokcho =
qotor.daiin.chotaiin/sokchor.qokoiiin (f37v);
otchol.chol.chol.daiin.chotaiin/s,o,kchol.chol.chol.daiin (f56v)
But sometimes they don’t. A sequence that appears once within a line might appear elsewhere split across a line break or even a page break.
- olchedyqokainolsheyqokain =
qol.ol,oiin,olkain.ol.chedy.qokain.olshey.qokain/ (f50v);
qokain.dal.tol.olchedy/qokain.olshey.qokain.darol (f75v) - daiindaiinqotchyqot =
odaiin.daiin.qotchy.qotor (f10r);
daiin.daiin/qotchy.qoteey (f37v) - chodaiinqokcheodych =
qotol.chodaiin.qokcheody.cho,r.chod-ycthol.s.olcheety (f51v);
daiin.chodaiin (f89r1, at end of page within foldout structure, followed by:) qokcheody.cheodal (f89r2)
These latter cases suggest that line breaks don’t always disrupt line-internal patterns, and that the text can sometimes continue seamlessly across them as though they weren’t there. But it’s also notable that in all three of the paired examples cited above, the occurrence with a line or page break inserts it immediately before q. We’ve already established that line-initial q is constrained to an unusual degree by the ending of the preceding line, especially in its lower probability after a line ending with m. Perhaps whatever factor is responsible for that behavior also permits a sequence to “break” at q without disrupting whatever contextual or structural relationships it would have if it had all fallen within the same line.
In addition to the broad distinction between Currier A and Currier B, and the distinctions among smaller sections such as Quire 13 and Quire 20, there are other localized anomalies that seem to affect probabilities on the level of whole pages (with multiple paragraphs). Some pages display unusually high concentrations of certain glyphs (e.g., m on f3r and f3v, ch on f56r, k on f40r), while others have unusually low concentrations of certain glyphs (e.g., there are no tokens of e+ on f14v, f22v, f36r, and only one—always e—on each of f11r, f13v, and f19r; and there are no tokens of n on f27v and only one on f41r). From the perspective of transitional probabilities, these cases can be analyzed in terms of particular transitions being bolstered or inhibited not just within a line, or a paragraph, but across a whole page. If we calculate transitional probabilities for the subset of six pages I mentioned with low or zero counts of e+, and compare them against probabilities for Currier A in general, we find that the decrease in probability of a transition to e+ on these pages coincides with an increase in probability of transition to specific alternatives, especially y and Sh.
- All Currier A: ch>o (45.67%), ch>e+ (25.10%), ch>y (14.69%), ch>a (6.54%)
- Subset: ch>o (61=42.96%), ch>y (58=40.85%), ch>a (8=5.63%), ch>e+ (4=2.82%)
- All Currier A: Sh>o (46.61%), Sh>e+ (32.49%), Sh>y (10.57%), Sh>a (4.81%)
- Subset: Sh>o (23=52.27%), Sh>y (16=36.36%), Sh>a (1=2.27%), Sh>e+ (1=2.27%)
- All Currier A: k>e+ (30.43%), k>ch (19.59%), k>o (17.96%), k>a (16.87%), k>y (9.57%), k>Sh (4.23%)
- Subset: k>ch (28=35.90%), k>y (20=25.64%), k>o (12=15.38%), k>Sh (10=12.82%), k>a (7=8.97%)
- All Currier A: t>ch (30.87%), t>o (22.01%), t>a (15.77%), t>e+ (13.29%), t>y (12.28%), t>Sh (4.23%)
- Subset: t>ch (40=45.98%), t>y (20=22.99%), t>a (13=14.94%), t>o (9=10.34%), t>Sh (3=3.45%)
The same six pages happen to display a closed oldaiin loop (albeit only by a hair: n>o at 13=21.31% is stronger than n>ch at 7=11.48%), so I suppose we could tentatively define an Oldaiinese subdialect—maybe intermediary between Choldaiinese and Olese—and look for additional pages that conform to it. But even more thought-provoking, I think, is the possibility that such “languages” might themselves be nothing more than effects of contextual constraints comparable to the ones we’ve been examining, but unfolding on an especially grand scale—one extending across not just lines, not just paragraphs, and not just pages, but whole quires.
Conclusion
In this post, I’ve experimented with analyzing Voynichese in terms of glyph-by-glyph transitional probabilities as an alternative to “word grammar.” My feeling is more and more that the conspicuously regular structure of Voynichese words might be a red herring, and that it’s only by breaking apart the word as an object of study that we can gain a productive vantage point on other levels of patterning that are no less striking than those of words. I don’t mean to be dogmatic about the specific tack I’ve taken (although I like how minor changes in transitional probabilities can have cascading effects); I just think this may need to happen somehow. I agree that there must be some significance to spacing—to strong breakpoints and ambivalent breakpoints—but I suspect that this will prove to be no more central to the underlying scheme than is the punctuation of long numbers with commas or periods, and that word structure is epiphenomenal. Counterarguments welcome!
I’ve used EVA glyph definitions and limited myself to a linear analysis, which runs contrary to my own sense of how the script works (see here at sections two and three for some of my thoughts about that), but which I hope will make what I’ve written more accessible and more readily comparable with other studies.


















